AIS3 EOF CTF Quals 2021 WriteUps

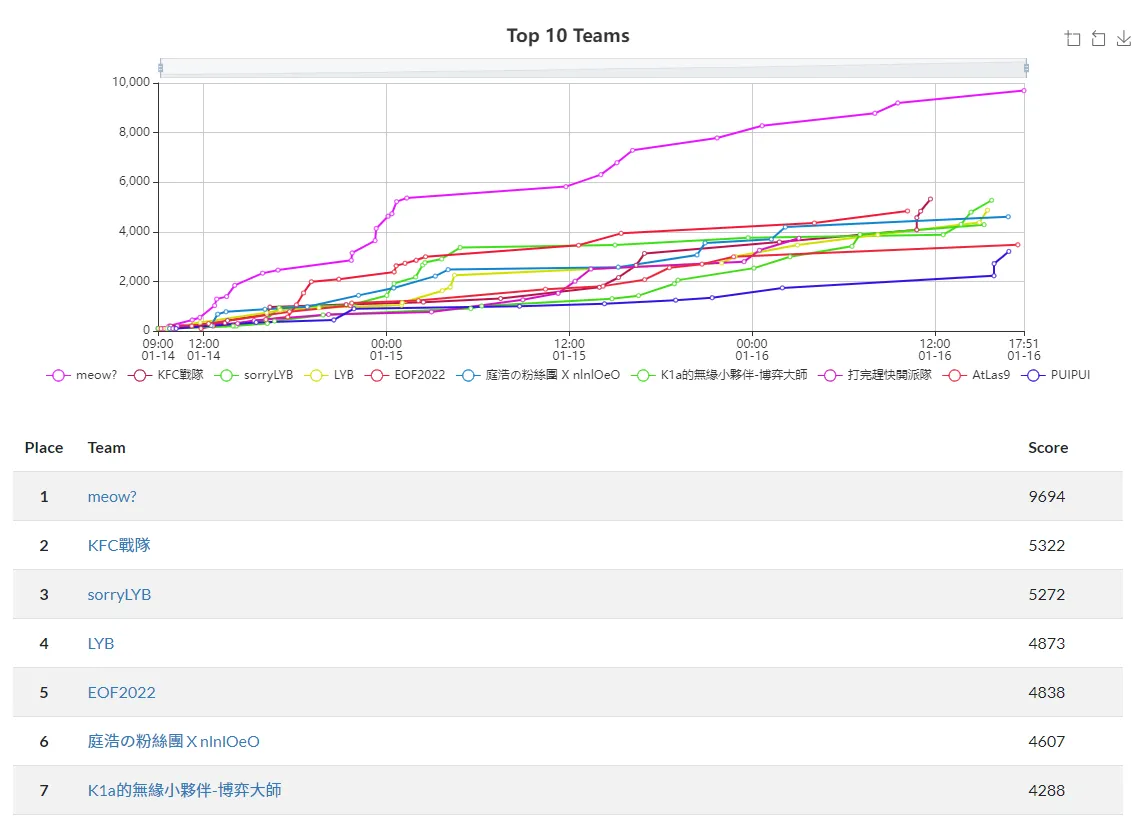
這次作為程安的期末考在 meow? 隊伍參加了 AIS3 EOF CTF 2021 Quals 拿了第一，也成功完全破台。這邊有全隊整合的 writeup，不過還是在這邊發一下自己解的一些題目。兩邊在內容上可能有些不同，以這邊為準。

 

Crypto

babyPRNG

from flag import flag
import random
import string

charset = string.ascii_letters + string.digits + '_{}'

class MyRandom:
	def __init__(self):
		self.n = 2**256
		self.a = random.randrange(2**256)
		self.b = random.randrange(2**256)

	def _random(self):
		tmp = self.a
		self.a, self.b = self.b, (self.a * 69 + self.b * 1337) % self.n
		tmp ^= (tmp >> 3) & 0xde
		tmp ^= (tmp << 1) & 0xad
		tmp ^= (tmp >> 2) & 0xbe
		tmp ^= (tmp << 4) & 0xef
		return tmp

	def random(self, nbit):
		return sum((self._random() & 1) << i for i in range(nbit))

assert all(c in charset for c in flag)
assert len(flag) == 60

random_sequence = []
for i in range(6):
	rng = MyRandom()
	random_sequence += [rng.random(8) for _ in range(10)]

ciphertext = bytes([x ^ y for x, y in zip(flag.encode(), random_sequence)])
print(ciphertext.hex())

這題的 PRNG 有兩個 256 bit 狀態 ，每次輸出時都會用 和 去更新。之後拿原本的 做一些 tamper 後輸出，取 lsb 作為輸出。

Tamper 的部份可以用觀察或是測試發現說 tmp 的 lsb 都保持不動，所以 tmp 的 lsb 直接就來自 :

tmp ^= (tmp >> 3) & 0xde
tmp ^= (tmp << 1) & 0xad
tmp ^= (tmp >> 2) & 0xbe
tmp ^= (tmp << 4) & 0xef

因為我們只在意 lsb，也就是 ，因為 的所以可以直接把 % self.n 視為 % 2，然後就可以注意到說 的 lsb 只和 有關。

所以在只考慮 lsb 的情況下這個 PRNG 實際上的狀態只有四種: 0 0 0 1 1 0 1 1

所以直接爆破四種起始狀態輸出的 key stream 即可 xor 回原本的 flag。

class MyRandom:
    def __init__(self, a, b):
        self.n = 2 ** 256
        self.a = a
        self.b = b

    def _random(self):
        tmp = self.a
        self.a, self.b = self.b, (self.a * 69 + self.b * 1337) % self.n
        tmp ^= (tmp >> 3) & 0xDE
        tmp ^= (tmp << 1) & 0xAD
        tmp ^= (tmp >> 2) & 0xBE
        tmp ^= (tmp << 4) & 0xEF
        return tmp

    def random(self, nbit):
        return sum((self._random() & 1) << i for i in range(nbit))


def xor(a, b):
    return bytes([x ^ y for x, y in zip(a, b)])


keys = [
    bytes([rng.random(8) for _ in range(10)])
    for a in range(2)
    for b in range(2)
    if (rng := MyRandom(a, b))
]
ct = bytes.fromhex(
    "9dfa2c9ccd5c84c61feb00ea835e848732ac8701da32b5865a84db59b08532b6cf32ebc10384c45903bf860084d018b5d55a5cebd832ef8059ead810"
)
for i in range(0, len(ct), 10):
    for k in keys:
        s = xor(ct[i : i + 10], k)
        if s.isascii():
            print(s.decode(), end="")
print()

# FLAG{1_pr0m153_1_w1ll_n07_m4k3_my_0wn_r4nd0m_func710n_4641n}

almostBabyPRNG

from flag import flag
import random


class MyRandom:
    def __init__(self):
        self.n = 256
        self.a = random.randrange(256)
        self.b = random.randrange(256)

    def random(self):
        tmp = self.a
        self.a, self.b = self.b, (self.a * 69 + self.b * 1337) % self.n
        tmp ^= (tmp >> 3) & 0xDE
        tmp ^= (tmp << 1) & 0xAD
        tmp ^= (tmp >> 2) & 0xBE
        tmp ^= (tmp << 4) & 0xEF
        return tmp


class TruelyRandom:
    def __init__(self):
        self.r1 = MyRandom()
        self.r2 = MyRandom()
        self.r3 = MyRandom()
        print(self.r1.a, self.r1.b)
        print(self.r2.a, self.r2.b)
        print(self.r3.a, self.r3.b)

    def random(self):
        def rol(x, shift):
            shift %= 8
            return ((x << shift) ^ (x >> (8 - shift))) & 255

        o1 = rol(self.r1.random(), 87)
        o2 = rol(self.r2.random(), 6)
        o3 = rol(self.r3.random(), 3)
        o = (~o1 & o2) ^ (~o2 | o3) ^ (o1)
        o &= 255
        return o


assert len(flag) == 36

rng = TruelyRandom()
random_sequence = [rng.random() for _ in range(420)]

for i in range(len(flag)):
    random_sequence[i] ^= flag[i]

open("output.txt", "w").write(bytes(random_sequence).hex())

這題使用的 PRNG TruelyRandom 是使用三個 MyRandom 所組合而成的，每個各有 種初始狀態。

輸出的時候是把每個 random 輸出的一個 byte 經過 rol 對 bits 做些交換，之後使用 o = (~o1 & o2) ^ (~o2 | o3) ^ (o1) 的做組合後輸出一個 byte。因為不是 lsb 所以不能像前面那題直接 。

直接爆破的話需要 次才能找出初始的狀態，雖然可能用 C/C++ 加上一些平行化應該有機會解出來，但顯然不是預期的解法。

先觀察輸出公式的真值表可以看出說 o1 和 ~o 有 75% 的機率相同，o3 和 ~o 也是 75% 的機率相同。在這種情況下就能使用 correlation attack 去單獨爆破其中一個 MyRandom 的 seed，只需要 次。

由於輸出的值是一個 byte，在 correlation attack 的時候是直接比較 8 個 bits 相同的機率，然後取平均看有沒有超過 70%。

獲得 r1 和 r3 的 seed 之後直接再用 爆破出 r2 的 seed，之後就能 xor 回原本的 flag。

class MyRandom:
    def __init__(self, a, b):
        self.a = a
        self.b = b

    def random(self):
        tmp = self.a
        self.a, self.b = self.b, (self.a * 69 + self.b * 1337) & 0xFF
        tmp ^= (tmp >> 3) & 0xDE
        tmp ^= (tmp << 1) & 0xAD
        tmp ^= (tmp >> 2) & 0xBE
        tmp ^= (tmp << 4) & 0xEF
        return tmp


def rol(x, shift):
    shift %= 8
    return ((x << shift) ^ (x >> (8 - shift))) & 255


ct = list(
    bytes.fromhex(
        "d5de8acdc0fa83d9c5bbe683cb33ef07949d6faeee8b00f6a2cc10cad800ca818e1cfd34f96f8fe71c9dbb3930ec8fb89183c9eef059cddcdc62a3fcf96eaea6dcab1bde96db8dbb13e3eb5d144fec9c6c91637cffdb0d8c988c2a189a8aaeaa136afe8cd469dddedf88ed7effbf2fd89e8f8afa88beb9ba1150eaaec0c8fdb5d4fbe3efff8ca866ecbf2bda996a7f9e136d6d6e1afbccb664e24d5ef98e9fa63e8d8b3a385aef999389d9dcfbe9f8f6d4908bdaf9bdbd8dfeaebafea28aca8c9181cb8ca8cbc9a6f48893dcf94b8b4efca91a8ab1a84f9893ac4fafb86ee9dbff7a9949ff6e8fe40a9daa2c30ea99b89383c9ecf459d8d8dc66a1fcff6daeb4caab0ad896c88cbb11e3eb4c134ff9886c84617cf9cf0d8b9d8c3b189a88adaa117dfe8ac369c8c9df88f87ef9ad2fce9f8f9be988a9adba1343eabbd6c8e8b4d4eaf2eff989a865febf3acb996c6d9e11696d6c1afbd9b664e64b5eff899fb42c8d9a383849ea99918dd9cdf8e9ede6d4858ddaffadbd8affaeabfaa288cd8c9392cb8abbcbdcb5f48882dcff5d8b58f9a90b9db1bf5f9891bb4fbaaa6efcdeff6b8c49"
    )
)


def gen_table(shift, ln=128):
    table = {}

    for a in range(256):
        for b in range(256):
            r = MyRandom(a, b)
            stream = tuple([rol(r.random(), shift) for _ in range(ln)])
            table[stream] = (a, b)
    return table


def solve_gen1():
    # a == ~(((~a)&b)^((~b)|c)^a) for 75%
    table = gen_table(87)
    for stream, (a, b) in table.items():
        same = [0] * 8
        for i in range(36, len(stream)):
            for j in range(8):
                mask = 1 << j
                if ((~ct[i]) & mask) == stream[i] & mask:
                    same[j] += 1
        rates = [s / (len(stream) - 36) for s in same]
        if sum(rates) / len(rates) > 0.70:
            print(a, b, rates)
            return a, b, stream


def solve_gen3():
    # c == ~(((~a)&b)^((~b)|c)^a) for 75%
    table = gen_table(3)
    for stream, (a, b) in table.items():
        same = [0] * 8
        for i in range(36, len(stream)):
            for j in range(8):
                mask = 1 << j
                if ((~ct[i]) & mask) == stream[i] & mask:
                    same[j] += 1
        rates = [s / (len(stream) - 36) for s in same]
        if sum(rates) / len(rates) > 0.70:
            print(a, b, rates)
            return a, b, stream


a1, b1, s1 = solve_gen1()
a3, b3, s3 = solve_gen3()
table2 = gen_table(6)
for s2, (a2, b2) in table2.items():
    oo = [((~o1 & o2) ^ (~o2 | o3) ^ (o1)) & 0xFF for o1, o2, o3 in zip(s1, s2, s3)]
    if oo[36:] == ct[36 : len(oo)]:
        print(a2, b2)
        print(bytes([x ^ y for x, y in zip(oo, ct)][:36]))

# pypy3 takes less than 3s
# FLAG{1_l13d_4nd_m4d3_4_n3w_prn6_qwq}

notRSA

from Crypto.Util.number import *
from secret import flag

n = ZZ(bytes_to_long(flag))
p = getPrime(int(640))
assert n < p
print(p)

K = Zmod(p)

def hash(B, W, H):
    def step(a, b, c):
        return vector([9 * a - 36 * c, 6 * a - 27 * c, b])
    def steps(n):
        Kx.<a, b, c> = K[]
        if n == 0: return vector([a, b, c])
        half = steps(n // 2)
        full = half(*half)
        if n % 2 == 0: return full
        else: return step(*full)
    return steps(n)(B, W, H)

print(hash(79, 58, 78))

這題只給了個 hash function，輸入有 和三個常數 ，其中 是 flag。step 函數單純的對於三個輸入 輸出一個向量 。計算一律在一個 下運算。

steps 函數則是對於輸入 使用 symbolic 的 做一些運算，仔細一看可以看出那其實是很單純的快速冪。假設 step 代表的是一個未知的轉換 ，half = steps(n // 2) 計算 ，然後 half(*half) 就是 ，之後看 的奇偶決定要不要多乘 。所以 steps(n) 其實就代表 而已。

而 step 代表的 本身其實很容易看出來是個矩陣乘法:

因此這題簡單來說就是給予 求 ，有點像是 discrete log。

要求矩陣的次方想做的第一件事是對角化看看，不過很容易就能發現 不可對角化，只能算 jordan form 而已，也就是求出 ，其中 是個上三角矩陣。

另外 ，所以 可以化為 ，其中 和 。

這題的 是:

上三角矩陣的次方容易推出通項公式，不過我直接偷懶讓 WolframAlpha 大神來計算: 通項公式

所以

其中 和 分別是 的三個維度，都是已知的值。因為 未知所以設成 方便處裡，待會消掉:

相除得到

所以

from Crypto.Util.number import *

p = 2888665952131436258952936715089276376855255923173168621757807730410786288318040226730097955921636005861313428457049105344943798228727806651839700038362786918890301443069519989559284713392330197
K = Zmod(p)
A = matrix(K, [[9, 0, -36], [6, 0, -27], [0, 1, 0]])
u = vector(K, (79, 58, 78))
v = vector(
    K,
    (
        2294639317300266890015110188951789071529463581989085276295636583968373662428057151776924522538765000599065000358258053836419742433816218972691575336479343530626038320565720060649467158524086548,
        1566616647640438520853352451277215019156861851308556372753484329383556781312953384064601676123516314472065577660736308388981301221646276107709573742408246662041733131269050310226743141102435560,
        2794094290374250471638905813912842135127051843020655371741518235633082381443339672625718699933072070923782732400527475235532783709419530024573320695480648538261456026723487042553523968423228485,
    ),
)
J, P = A.jordan_form(transformation=True)
# A^n*v=u
# A=PJP^-1
# J^n*vv=uu
print(J)
vv = ~P * v
uu = ~P * u
a, b, c = uu
aa, bb, cc = vv
n = (18 * bb * c - 18 * b * cc) / (6 * c * cc)
print(long_to_bytes(n))

# FLAG{haha_diagonalization_go_brRRRrRrrrRrRrrrRrRrRRrrRrRrRRRRrrRRrRRrrrrRrRrRrR}

babyRSA

from Crypto.Util.number import *
from secret import flag

p = getPrime(512)
q = getPrime(512)
n = p * q
m = n**2 + 69420
h = (pow(3, 2022, m) * p**2 + pow(5, 2022, m) * q**2) % m
c = pow(bytes_to_long(flag), 65537, n)

print('n =', n)
print('h =', h)
print('c =', c)

這題是在一般 RSA 之上多提供一個 ，其中 , , 。

都是 512 bits，所以 是 1024 bits，而 是 2048 bits。所以可以寫出下方的 Lattice basis:

註: 本文中 Lattice 一律以 row vector 為 basis

可知 存在這個 Lattice 中，其中只有 已知，其他只知道 而已。所以可以寫出 的上下界 和 。

一個簡單的想法是用 LLL 對 reduce 過之後使用 Babai nearest plane 去近似 ，只是會發現求出來的 和實際上的 差很大。解決辦法和 LLL 會去調整權重一樣，把第一個 column 乘上很大的值就可以讓 reduced basis 的第一維變很小。在 CVP 的話因為我們已經很肯定第一維就是 ，所以讓 reduced basis 的第一維夠小才比較好的逼近目標向量。

這個技巧就在 rkm0959/Inequality_Solving_with_CVP 這個 repo 中實作了出來，方法就是把 差很小的維度乘上很大的值，反之差很大的維度就讓它乘上比較小的值。這樣 reduced basis 就會根據目標的上下界差值有大和小的變化，更容易找出目標的 。

使用了那個 repo 的 CVP solver 出來的向量 根據自己測試有大概 的機率下第二維是個完全平方數 ，就算不是也可以拿 reduced basis 的前兩短向量 出來，暴力搜尋附近的向量，也就是 。根據測試大概 99% 都能找到目標的 ，即可成功分解 解密 flag。

註: 因為 ，所以 才會是完全平方數

from Crypto.Util.number import *

n = 60116508546664196727889673537793426957208317552814539722187167053623876043252780386821990827068176541032744152377606007460695865230455445490316090376844822501259106343706524194509410859747044301510282354678419831232665073515931614133865254324502750265996406483174791757276522461194898225654233114447953162193
h = 2116009228641574188029563238988754314114810088905380650788213482300513708694199075187203381676605068292187173539467885447061231622295867582666482214703260097506783790268190834638040582281613892929433273567874863354164328733477933865295220796973440457829691340185850634254836394529210411687785425194854790919451644450150262782885556693980725855574463590558188227365115377564767308192896153000524264489227968334038322920900226265971146564689699854863767404695165914924865933228537449955231734113032546481992453187988144741216240595756614621211870621559491396668569557442509308772459599704840575445577974462021437438528
c = 50609945708848823221808804877630237645587351810959339905773651051680570682896518230348173309526813601333731054682678018462412801934056050505173324754946000933742765626167885199640585623420470828969511673056056011846681065748145129805078161435256544226137963588018603162731644544670134305349338886118521580925
e = 65537
m = n ** 2 + 69420
a = pow(3, 1011, m)
b = pow(5, 1011, m)

B = matrix(ZZ, [[m, 0, 0], [a ^ 2, 1, 0], [b ^ 2, 0, 1]])

load("solver.sage")  # https://github.com/rkm0959/Inequality_Solving_with_CVP
lb = [h, 0, 0]
ub = [h, 2 ^ 1024, 2 ^ 1024]
result, applied_weights, fin = solve(B, lb, ub)  # PS: B will be modified inplace
v = vector(
    [x // y for x, y in zip(result, applied_weights)]
)  # closest vector to (lb+ub)/2
print(v)
if not v[1].is_square():
    R = B.LLL()
    l0 = vector([x // y for x, y in zip(R[0], applied_weights)])
    l1 = vector([x // y for x, y in zip(R[1], applied_weights)])
    # enumerate nearby vectors
    for i in range(-10, 10):
        for j in range(-10, 10):
            vv = v + l0 * i + l1 * j
            if vv[1].is_square():
                print("found", i, j)
                p = vv[1].sqrt()
                q = vv[2].sqrt()
                assert p * q == n
                d = inverse_mod(e, (p - 1) * (q - 1))
                m = power_mod(c, d, n)
                print(long_to_bytes(m))
# FLAG{7hI5_i5_4_C0MPL373_r4nD0M_fL49_8LinK}

easyRSA

from Crypto.Util.number import *
import os

from flag import flag

blen = 256

def rsa(p: int, q: int, message: bytes):
	n = p * q
	e = 65537
	
	pad_length = n.bit_length() // 8 - len(message) - 2 # I padded too much
	message += os.urandom(pad_length)
	m = bytes_to_long(message)
	return (n, pow(m, e, n))

def level1(message1: bytes, message2: bytes):
	while True:
		p1 = getPrime(blen) # 512-bit number
		p2 = (p1 - 1) // 2
		if isPrime(p2):
			break

	q1 = getPrime(blen)
	q2 = getPrime(blen)

	return rsa(p1, q1, message1), rsa(p2, q2, message2)

def level2(message1: bytes, message2: bytes):
	while True:
		p1 = getPrime(blen) # 512-bit number
		p2 = (p1 + 1) // 2
		if isPrime(p2):
			break

	q1 = getPrime(blen)
	q2 = getPrime(blen)

	return rsa(p1, q1, message1), rsa(p2, q2, message2)

assert len(flag) == 44
l = len(flag) // 4
m1, m2, m3, m4 = [flag[i * l: i * l + l] for i in range(4)]
c1, c2 = level1(m1, m2)
c3, c4 = level2(m3, m4)

print(f'{c1 = }')
print(f'{c2 = }')
print(f'{c3 = }')
print(f'{c4 = }')

這題的 flag 分成了四等分，分別用了四個 RSA modulus 加密，前兩個是 level1，後兩個是 level2。

level1

解題可以從費馬小定理開始

可知就算多開 次方也成立

而 是 的倍數，所以 ，因此 對於大部分的 成立。

只是說 是個很大的數字，沒辦法對任意整數開 次方，需要 才行，所以是

之所以能這樣做是因為 ，如果不整除的話就不能這樣 ，這是因為有下方的這個性質才能這麼做的:

這個概念其實就是 Pollard p-1，當 夠 smooth 的時候可以隨便乘一堆小的質數得到 ，如果 的話就開 次方就能分解了。這題只是利用 提供給你了 的倍數方便分解。

level2

唯一的不同在於 變成了 ，看到 就比較容易想到和 Pollard p-1 相對的 Williams p+1 分解法。

參考這篇文章可知對於以下的 Lucas Sequence

設 ，若 時則有 ，其中 是 的倍數，而 是 Legendre symbol。

如果 不是 的二次剩餘，那 ，所以只要 是 的倍數就能分解 了。而 顯然是 的倍數。

可以直接隨便猜 ，機率大概 不是二次剩餘。剩下就是該如何計算 了，這部分和前面一樣可以 避免數字太大。只是直接按照上面給的遞迴公式計算需要 才能得到 ，對於 來說太慢了。

這邊可以注意到 其實類似費氏數列，可以直接用矩陣快速冪在 算出第 項，然後之後 後就能算出 解密。

from Crypto.Util.number import *

c1 = (
    7125334583032019596749662689476624870348730617129072883601037230619055820557600004017951889099111409301501025414202687828034854486218006466402104817563977,
    4129148081603511890044110486860504513096451540806652331750117742737425842374298304266296558588397968442464774130566675039127757853450139411251072917969330,
)
c2 = (
    2306027148703673165701737115582071466907520373299852535893311105201050695517991356607853174423460976372892149320885781870159564414187611810749699797202279,
    600009760336975773114176145593092065538518609408417314532164466316030691084678880434158290740067228766533979856242387874408357893494155668477420708469922,
)
c3 = (
    9268888642513284390417550869139808492477151321047004950176038322397963262162109301251670712046586685343835018656773326672211744371702420113122754069185607,
    5895040809839234176362470150232751529235260997980339956561417006573937337637985480242398768934387532356482504870280678697915579761101171930654855674459361,
)
c4 = (
    6295574851418783753824035390649259706446806860002184598352000067359229880214075248062579224761621167589221171824503601152550433516077931630632199823153369,
    3120774808318285627147339586638439658076208483982368667695632517147182809570199446305967277379271126932480036132431236155965670234021632431278139355426418,
)
e = 65537


def solve_level1(n1, c1, n2, c2):
    p1 = gcd(power_mod(2, 2 * n2, n1) - 1, n1)
    p2 = (p1 - 1) // 2
    q1 = n1 // p1
    q2 = n2 // p2
    d1 = inverse_mod(e, (p1 - 1) * (q1 - 1))
    d2 = inverse_mod(e, (p2 - 1) * (q2 - 1))
    m1 = power_mod(c1, d1, n1)
    m2 = power_mod(c2, d2, n2)
    return long_to_bytes(m1), long_to_bytes(m2)


def lucas_v(a, n):
    # computes n-th lucas number for v_n=a*v_{n-1}-v_{n-2} with fast matrix power
    v0 = 2
    v1 = a
    R = a.base_ring()
    M = matrix(R, [[a, -1], [1, 0]])
    v = M ^ (n - 1) * vector(R, [v1, v0])
    return v[0]


def solve_level2(n1, c1, n2, c2):
    # based on Williams p+1: http://users.telenet.be/janneli/jan/factorization/williams_p_plus_one.html
    for a in range(2, 10):
        p1 = ZZ(gcd(lucas_v(Mod(a, n1), 2 * n2) - 2, n1))
        if 1 < p1 < n1:
            break
    p2 = (p1 + 1) // 2
    q1 = n1 // p1
    q2 = n2 // p2
    d1 = inverse_mod(e, (p1 - 1) * (q1 - 1))
    d2 = inverse_mod(e, (p2 - 1) * (q2 - 1))
    m1 = power_mod(c1, d1, n1)
    m2 = power_mod(c2, d2, n2)
    return long_to_bytes(m1), long_to_bytes(m2)


m1, m2 = solve_level1(*c1, *c2)
m3, m4 = solve_level2(*c3, *c4)

flag = b"".join([x[:11] for x in [m1, m2, m3, m4]])
print(flag)

# flag{S0rry_1_f0r9ot_T0_cH4nGe_7h3_t35t_fl46}

延伸說明

Williams p+1 的原理基本上是把運算轉移到 上。概念上類似於 擴充到 時是多一個 符合 。如果 的話 是 irreducible，這樣才能 reduce 到 的 field 中。

由於 的 multiplicative order 是 ，所以有不同 subgroup 的問題。推導一下可以知道:

當開 次方的時候虛部消失了，代表它是 的倍數，用 gcd 即可分解出來。

如果 的話 ，那麼:

虛部一樣也消失了，所以一樣可以用 gcd 分解，這代表 Williams p+1 也能處裡 p-1 的 case。不過原版的 Pollard p-1 是使用實部已知的的 去 gcd 的。

使用 sage 做個簡單的驗證:

p = random_prime(2 ^ 512)
q = random_prime(2 ^ 512)
n = p * q
P.<x> = Zmod(n)[]


def test(T):
    print("QR", kronecker(T, p))
    R.<i> = P.quotient(x^2 - T)
    z = 1 + i
    print("p-1", gcd((z ^ (p - 1))[1], n))
    print("p+1", gcd((z ^ (p + 1))[1], n))


T = next(x for x in range(2, 100) if kronecker(x, p) == 1)
test(T)
T = next(x for x in range(2, 100) if kronecker(x, p) == -1)
test(T)

而原版的 Williams p+1 使用了 lucas sequence 也是做同一件事，只是改用了遞迴數列去計算 的高次方。

對於這個遞迴數列的特徵多項式 可以算出兩根，然後帶入初始項能求出常數 ，所以得通項公式為:

考慮 的話可知 其實就是那個 ，根據是否是二次剩餘決定是 還是 的關鍵。一樣考慮 的情況 可以推出

把它換成 的倍數也有一樣的結果，所以 會給出 。

這篇文章還有來自更加高等數學角度的說明，只是後半段的數學我真的理解不了...

notPRNG

from secret import flag
import sys

def genModular(x):
    if x <= 2 * 210:
        return random_prime(2^x, False, 2^(x - 1))
    return random_prime(2^210, False, 2^209) * genModular(x - 210)

N, L = 100, 200
M = genModular(int(N * N * 0.07 + N * log(N, 2)))

# generate a random vector in Z_M
a = vector(ZZ, [ZZ.random_element(M) for _ in range(N)])

# generate a random 0/1 matrix
while True:
    X = Matrix(ZZ, L, N)
    for i in range(L):
        for j in range(N):
            X[i, j] = ZZ.random_element(2)
    if X.rank() == N:
        break

# let's see what will this be
b = X * a
for i in range(L):
    b[i] = mod(b[i], M)

print('N =', N)
print('L =', L)
print('M =', M)
print('b =', b)

x = vector(ZZ, int(N))
for j in range(N):
    for i in range(L):
        x[j] = x[j] * 2 + X[i, j]



def bad():
    print("They're not my values!!!")
    sys.exit(0)

def calc(va, vx):
    ret = [0] * L
    for i, vai in enumerate(va):
        for j in range(L):
            bij = (vx[i] >> (L - 1 - j)) & 1
            ret[j] = (ret[j] + vai * bij) % M
    return ret


if __name__ == '__main__':
    print('What are my original values?')
    print('a?')
    aa = list(map(int, input().split()))
    print('x?')
    xx = list(map(int, input().split()))

    if len(aa) != len(a):
        bad()
    if len(xx) != len(x):
        bad()
    if calc(a, x) != calc(aa, xx):
        bad()

    print(flag)

程式碼有點複雜，但簡單來說就是給予你向量 和大整數 ，求矩陣 和向量 符合 。其中 指定說每個元素都只能是 ，且 。

Source code 中下面這段是用來把 的 矩陣壓縮的

x = vector(ZZ, int(N))
for j in range(N):
    for i in range(L):
        x[j] = x[j] * 2 + X[i, j]

而 calc 函數其實就只是利用壓縮過的矩陣 vx 和向量 va 做 而已。

這個問題的 是個 的矩陣， 是 向量， 是 向量。其中 。可知如果 的話有個很簡單的 trivial solution，就是 取單位矩陣 ，而 。只是這題難就難在 這件事上。

這題就像是在問說怎麼把個 維的 向量拆成 個只由 組成的 basis，一時之間真的想不到怎麼做。不過可以觀察到說如果 已知，那這個問題就變成了解 個 subset sum problem，雖然這問題在一般情況下是 NP-Complete 的，但是在 low density 的情況下可以利用 LLL 之類的算法在多項式時間內解決問題。(Solving Low-Density Subset Sum Problems)

以這題 的生成方式可以知道 density:

而對於 density 小於 的 subset sum problem 都是 LLL 可以處裡的(來源)，所以這題肯定和 LLL 脫不了關係。

解題的話目前有兩個方法，先找 或是先找 。先找 還不知道怎麼做，但任意固定 的話不一定能有 subset sum 的解這件事是已知的。就算找到了一個 確定對於 個 subset sum 都有解，需要重複解 次，經測試在我的電腦上解一個 subset sum 需要約 20 秒，而 秒過去的話肯定會 timeout，所以這方向不可行。

另一個出發點是想辦法尋找 ，有 的話就解方程組得到 ，但顯然不是對於任意的 矩陣都有解的。所以目標是要找個方法求出 ，找到的 矩陣不一定要和原本的 完全一樣也可以，就算是 basis 的順序有些交換也還是能夠解出一個 使得 的。

先用下面這個 Lattice 去 reduce:

其中空白部分都是 ， 是隨便選的一個大常數，讓 reduced 過的 basis 的第一維盡量保持為 。basis 中會有多個 型式的短向量。由於每個 都是來自 向量的一些 的線性組合，可以預期 其實都不會很大。

實際測試會發現 reduced 過的 basis 中的前 個向量的第一維都是 ，但只有前面 個向量的 大概都落在 的區間，剩下的都會遠遠超出這個範圍。把這 個 維向量視為一個 的矩陣 ，可知 。因為 ，所以 。

由於 都是 構成的， 裡面也大概落在