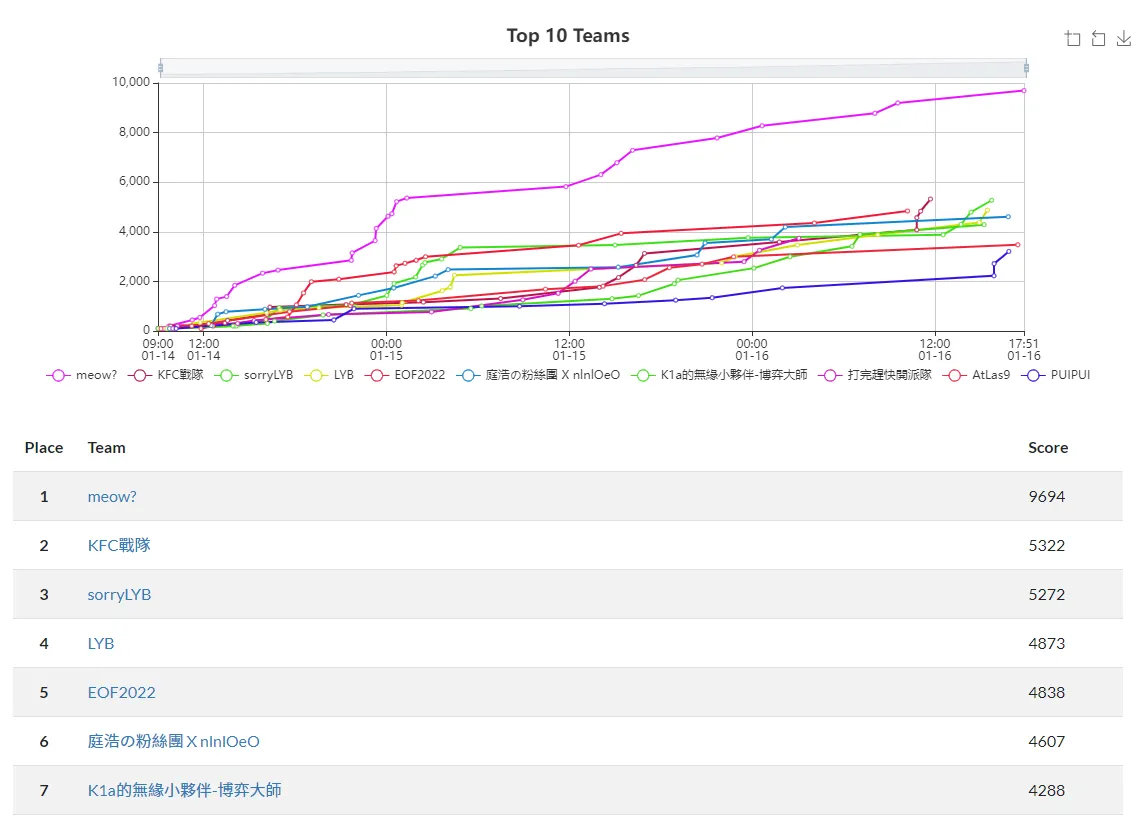
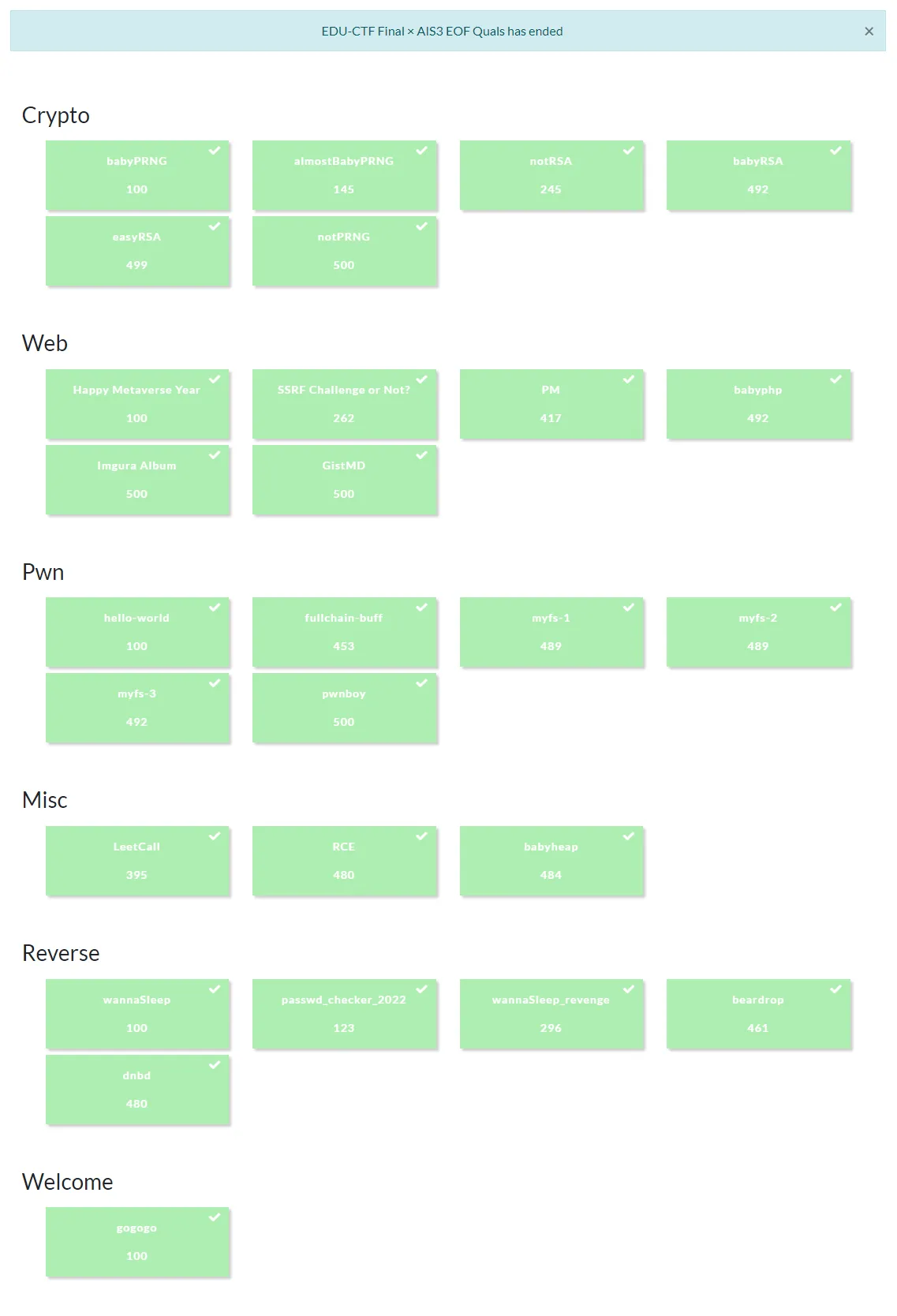
This time, as the final exam for the course, I participated in the AIS3 EOF CTF 2021 Quals with the team meow? and took first place, successfully solving all challenges. Here is the writeup integrated by the whole team, but I will still post some of the challenges I solved here. The content may differ between the two, so refer to this one.

Crypto#

babyPRNG#

from flag import flag
import random
import string

charset = string.ascii_letters + string.digits + '_{}'

class MyRandom:
	def __init__(self):
		self.n = 2**256
		self.a = random.randrange(2**256)
		self.b = random.randrange(2**256)

	def _random(self):
		tmp = self.a
		self.a, self.b = self.b, (self.a * 69 + self.b * 1337) % self.n
		tmp ^= (tmp >> 3) & 0xde
		tmp ^= (tmp << 1) & 0xad
		tmp ^= (tmp >> 2) & 0xbe
		tmp ^= (tmp << 4) & 0xef
		return tmp

	def random(self, nbit):
		return sum((self._random() & 1) << i for i in range(nbit))

assert all(c in charset for c in flag)
assert len(flag) == 60

random_sequence = []
for i in range(6):
	rng = MyRandom()
	random_sequence += [rng.random(8) for _ in range(10)]

ciphertext = bytes([x ^ y for x, y in zip(flag.encode(), random_sequence)])
print(ciphertext.hex())

This challenge's PRNG has two 256-bit states $a,b$, which are updated each time an output is generated using $a'=b$ and $b'=69a+1337b \bmod{2^{256}}$. The original $a$ is then tampered with and the lsb is taken as the output.

The tampering part can be observed or tested to find that the lsb of tmp remains unchanged, so the lsb of tmp directly comes from $a$:

tmp ^= (tmp >> 3) & 0xde
tmp ^= (tmp << 1) & 0xad
tmp ^= (tmp >> 2) & 0xbe
tmp ^= (tmp << 4) & 0xef

Since we only care about the lsb, which is $\bmod{2}$, and since $2|2^{256}$, we can directly treat % self.n as % 2, and then notice that the lsb of $b'$ only depends on $a,b$.

So, considering only the lsb, this PRNG actually has only four states: 0 0 0 1 1 0 1 1.

Therefore, we can brute force the key stream output for the four initial states and xor back to the original flag.

class MyRandom:
    def __init__(self, a, b):
        self.n = 2 ** 256
        self.a = a
        self.b = b

    def _random(self):
        tmp = self.a
        self.a, self.b = self.b, (self.a * 69 + self.b * 1337) % self.n
        tmp ^= (tmp >> 3) & 0xDE
        tmp ^= (tmp << 1) & 0xAD
        tmp ^= (tmp >> 2) & 0xBE
        tmp ^= (tmp << 4) & 0xEF
        return tmp

    def random(self, nbit):
        return sum((self._random() & 1) << i for i in range(nbit))


def xor(a, b):
    return bytes([x ^ y for x, y in zip(a, b)])


keys = [
    bytes([rng.random(8) for _ in range(10)])
    for a in range(2)
    for b in range(2)
    if (rng := MyRandom(a, b))
]
ct = bytes.fromhex(
    "9dfa2c9ccd5c84c61feb00ea835e848732ac8701da32b5865a84db59b08532b6cf32ebc10384c45903bf860084d018b5d55a5cebd832ef8059ead810"
)
for i in range(0, len(ct), 10):
    for k in keys:
        s = xor(ct[i : i + 10], k)
        if s.isascii():
            print(s.decode(), end="")
print()

# FLAG{1_pr0m153_1_w1ll_n07_m4k3_my_0wn_r4nd0m_func710n_4641n}

almostBabyPRNG#

from flag import flag
import random


class MyRandom:
    def __init__(self):
        self.n = 256
        self.a = random.randrange(256)
        self.b = random.randrange(256)

    def random(self):
        tmp = self.a
        self.a, self.b = self.b, (self.a * 69 + self.b * 1337) % self.n
        tmp ^= (tmp >> 3) & 0xDE
        tmp ^= (tmp << 1) & 0xAD
        tmp ^= (tmp >> 2) & 0xBE
        tmp ^= (tmp << 4) & 0xEF
        return tmp


class TruelyRandom:
    def __init__(self):
        self.r1 = MyRandom()
        self.r2 = MyRandom()
        self.r3 = MyRandom()
        print(self.r1.a, self.r1.b)
        print(self.r2.a, self.r2.b)
        print(self.r3.a, self.r3.b)

    def random(self):
        def rol(x, shift):
            shift %= 8
            return ((x << shift) ^ (x >> (8 - shift))) & 255

        o1 = rol(self.r1.random(), 87)
        o2 = rol(self.r2.random(), 6)
        o3 = rol(self.r3.random(), 3)
        o = (~o1 & o2) ^ (~o2 | o3) ^ (o1)
        o &= 255
        return o


assert len(flag) == 36

rng = TruelyRandom()
random_sequence = [rng.random() for _ in range(420)]

for i in range(len(flag)):
    random_sequence[i] ^= flag[i]

open("output.txt", "w").write(bytes(random_sequence).hex())

This challenge uses a PRNG TruelyRandom composed of three MyRandom, each with $256^2$ initial states.

The output is a byte from each random, which is then bitwise rotated and combined using o = (~o1 & o2) ^ (~o2 | o3) ^ (o1). Since it's not the lsb, we can't directly $\bmod{2}$ like the previous challenge.

Brute-forcing would require $(256^2)^3=2^{48}$ attempts to find the initial state, which might be possible with C/C++ and parallelization, but it's clearly not the intended solution.

Observing the output formula's truth table, we can see that o1 and ~o have a 75% chance of being the same, and o3 and ~o also have a 75% chance of being the same. In this case, we can use a correlation attack to individually brute force the seed of one MyRandom, requiring $256^{2}+256^{2}$ attempts.

Since the output is a byte, during the correlation attack, we compare the probability of 8 bits being the same and take the average to see if it exceeds 70%.

After obtaining the seeds of r1 and r3, we can brute force the seed of r2 with $256^{2}$ attempts, and then xor back to the original flag.

class MyRandom:
    def __init__(self, a, b):
        self.a = a
        self.b = b

    def random(self):
        tmp = self.a
        self.a, self.b = self.b, (self.a * 69 + self.b * 1337) & 0xFF
        tmp ^= (tmp >> 3) & 0xDE
        tmp ^= (tmp << 1) & 0xAD
        tmp ^= (tmp >> 2) & 0xBE
        tmp ^= (tmp << 4) & 0xEF
        return tmp


def rol(x, shift):
    shift %= 8
    return ((x << shift) ^ (x >> (8 - shift))) & 255


ct = list(
    bytes.fromhex(
        "d5de8acdc0fa83d9c5bbe683cb33ef07949d6faeee8b00f6a2cc10cad800ca818e1cfd34f96f8fe71c9dbb3930ec8fb89183c9eef059cddcdc62a3fcf96eaea6dcab1bde96db8dbb13e3eb5d144fec9c6c91637cffdb0d8c988c2a189a8aaeaa136afe8cd469dddedf88ed7effbf2fd89e8f8afa88beb9ba1150eaaec0c8fdb5d4fbe3efff8ca866ecbf2bda996a7f9e136d6d6e1afbccb664e24d5ef98e9fa63e8d8b3a385aef999389d9dcfbe9f8f6d4908bdaf9bdbd8dfeaebafea28aca8c9181cb8ca8cbc9a6f48893dcf94b8b4efca91a8ab1a84f9893ac4fafb86ee9dbff7a9949ff6e8fe40a9daa2c30ea99b89383c9ecf459d8d8dc66a1fcff6daeb4caab0ad896c88cbb11e3eb4c134ff9886c84617cf9cf0d8b9d8c3b189a88adaa117dfe8ac369c8c9df88f87ef9ad2fce9f8f9be988a9adba1343eabbd6c8e8b4d4eaf2eff989a865febf3acb996c6d9e11696d6c1afbd9b664e64b5eff899fb42c8d9a383849ea99918dd9cdf8e9ede6d4858ddaffadbd8affaeabfaa288cd8c9392cb8abbcbdcb5f48882dcff5d8b58f9a90b9db1bf5f9891bb4fbaaa6efcdeff6b8c49"
    )
)


def gen_table(shift, ln=128):
    table = {}

    for a in range(256):
        for b in range(256):
            r = MyRandom(a, b)
            stream = tuple([rol(r.random(), shift) for _ in range(ln)])
            table[stream] = (a, b)
    return table


def solve_gen1():
    # a == ~(((~a)&b)^((~b)|c)^a) for 75%
    table = gen_table(87)
    for stream, (a, b) in table.items():
        same = [0] * 8
        for i in range(36, len(stream)):
            for j in range(8):
                mask = 1 << j
                if ((~ct[i]) & mask) == stream[i] & mask:
                    same[j] += 1
        rates = [s / (len(stream) - 36) for s in same]
        if sum(rates) / len(rates) > 0.70:
            print(a, b, rates)
            return a, b, stream


def solve_gen3():
    # c == ~(((~a)&b)^((~b)|c)^a) for 75%
    table = gen_table(3)
    for stream, (a, b) in table.items():
        same = [0] * 8
        for i in range(36, len(stream)):
            for j in range(8):
                mask = 1 << j
                if ((~ct[i]) & mask) == stream[i] & mask:
                    same[j] += 1
        rates = [s / (len(stream) - 36) for s in same]
        if sum(rates) / len(rates) > 0.70:
            print(a, b, rates)
            return a, b, stream


a1, b1, s1 = solve_gen1()
a3, b3, s3 = solve_gen3()
table2 = gen_table(6)
for s2, (a2, b2) in table2.items():
    oo = [((~o1 & o2) ^ (~o2 | o3) ^ (o1)) & 0xFF for o1, o2, o3 in zip(s1, s2, s3)]
    if oo[36:] == ct[36 : len(oo)]:
        print(a2, b2)
        print(bytes([x ^ y for x, y in zip(oo, ct)][:36]))

# pypy3 takes less than 3s
# FLAG{1_l13d_4nd_m4d3_4_n3w_prn6_qwq}

notRSA#

from Crypto.Util.number import *
from secret import flag

n = ZZ(bytes_to_long(flag))
p = getPrime(int(640))
assert n < p
print(p)

K = Zmod(p)

def hash(B, W, H):
    def step(a, b, c):
        return vector([9 * a - 36 * c, 6 * a - 27 * c, b])
    def steps(n):
        Kx.<a, b, c> = K[]
        if n == 0: return vector([a, b, c])
        half = steps(n // 2)
        full = half(*half)
        if n % 2 == 0: return full
        else: return step(*full)
    return steps(n)(B, W, H)

print(hash(79, 58, 78))

This challenge provides a hash function with inputs $n$ and three constants $B,W,H$, where $n$ is the flag. The step function outputs a vector $[9a-36c,6a-27c,b]$ for three inputs $a,b,c$. All calculations are done in a $\mathbb{F}_p$ field.

The steps function uses symbolic $a,b,c$ for input $n$, which can be seen as simple exponentiation. Assuming step represents an unknown transformation $T$, half = steps(n // 2) calculates $T^{\lfloor{n/2}\rfloor}$, and half(*half) is $(T^{\lfloor{n/2}\rfloor})^2$. Depending on the parity of $n$, it may multiply by $T$. So steps(n) represents $T^n(x)$.

The step function itself can be seen as a matrix multiplication:

Thus, this challenge is about finding $n$ given $v=A^n u$, similar to a discrete log problem.

To find the matrix power, the first thing to try is diagonalization, but $A$ is not diagonalizable and can only be put in Jordan form, i.e., $A=PJP^{-1}$, where $J$ is an upper triangular matrix.

Additionally, $A^n=(PJP^{-1})^n=PJ^nP^{-1}$, so $v=A^n u$ can be transformed to $v'=J^n u'$, where $v'=P^{-1}v$ and $u'=P^{-1}u$.

The $J$ for this challenge is:

The general term formula for the power of an upper triangular matrix can be derived, but I used WolframAlpha for the calculation: General Term Formula

So

where $a,b,c$ and $a',b',c'$ are the three dimensions of $u'$ and $v'$, respectively, and are known values. Since $\frac{3^{n-2}}{2}$ is unknown, we set it as $k$ for convenience and eliminate it later:

Dividing gives

So

from Crypto.Util.number import *

p = 2888665952131436258952936715089276376855255923173168621757807730410786288318040226730097955921636005861313428457049105344943798228727806651839700038362786918890301443069519989559284713392330197
K = Zmod(p)
A = matrix(K, [[9, 0, -36], [6, 0, -27], [0, 1, 0]])
u = vector(K, (79, 58, 78))
v = vector(
    K,
    (
        2294639317300266890015110188951789071529463581989085276295636583968373662428057151776924522538765000599065000358258053836419742433816218972691575336479343530626038320565720060649467158524086548,
        1566616647640438520853352451277215019156861851308556372753484329383556781312953384064601676123516314472065577660736308388981301221646276107709573742408246662041733131269050310226743141102435560,
        2794094290374250471638905813912842135127051843020655371741518235633082381443339672625718699933072070923782732400527475235532783709419530024573320695480648538261456026723487042553523968423228485,
    ),
)
J, P = A.jordan_form(transformation=True)
# A^n*v=u
# A=PJP^-1
# J^n*vv=uu
print(J)
vv = ~P * v
uu = ~P * u
a, b, c = uu
aa, bb, cc = vv
n = (18 * bb * c - 18 * b * cc) / (6 * c * cc)
print(long_to_bytes(n))

# FLAG{haha_diagonalization_go_brRRRrRrrrRrRrrrRrRrRRrrRrRrRRRRrrRRrRRrrrrRrRrRrR}

babyRSA#

from Crypto.Util.number import *
from secret import flag

p = getPrime(512)
q = getPrime(512)
n = p * q
m = n**2 + 69420
h = (pow(3, 2022, m) * p**2 + pow(5, 2022, m) * q**2) % m
c = pow(bytes_to_long(flag), 65537, n)

print('n =', n)
print('h =', h)
print('c =', c)

This challenge provides an additional $h \equiv (ap)^2+(bq)^2 \pmod{m}$ on top of regular RSA, where $m=n^2+69420$, $a \equiv 3^{1011} \pmod{m}$, $b \equiv 5^{1011} \pmod{m}$.

$p,q$ are both 512 bits, so $n$ is 1024 bits, and $m$ is 2048 bits. We can write the following Lattice basis:

Note: In this article, Lattice is always represented as row vectors for the basis

We know that $v=(h,p^2,q^2)$ exists in this Lattice, where only $h$ is known, and the others are only known to be $0 \leq p^2,q^2 \leq 2^{1024}$. So we can write the bounds of $v$ as $\mathit{lb}=(h,0,0)$ and $\mathit{ub}=(h,2^{1024},2^{1024})$.

A simple idea is to use LLL to reduce $B$ and then use Babai's nearest plane to approximate $(\mathit{lb}+\mathit{ub})/2$, but we find that the resulting $h'$ differs significantly from the actual $h$. The solution is to adjust the weights, multiplying the first column by a large value to make the first dimension of the reduced basis very small. In CVP, since we are confident that the first dimension is $h$, making the first dimension of the reduced basis small helps approximate the target vector better.

This technique is implemented in the rkm0959/Inequality_Solving_with_CVP repo. The method is to multiply the dimensions with small differences in $\mathit{ub}-\mathit{lb}$ by large values and those with large differences by smaller values. This way, the reduced basis will have large and small variations based on the target's upper and lower bounds, making it easier to find the target $(lb+ub)/2$.

Using the CVP solver from that repo, the resulting vector $v$ has about a $\frac{1}{4} \sim \frac{1}{3}$ chance of having a perfect square $p^2$ in the second dimension. If not, we can take the first two short vectors $\lambda_1,\lambda_2$ from the reduced basis and brute force nearby vectors, i.e., $\{v+a\lambda_1+b\lambda_2 \mid a,b \in [-10,10]\}$. According to tests, about 99% of the time, we can find the target $p^2$, allowing us to factor $n$ and decrypt the flag.

Note: Since $p^2<m=n^2+69420$, $p^2\pmod{m}$ will be a perfect square.

from Crypto.Util.number import *

n = 60116508546664196727889673537793426957208317552814539722187167053623876043252780386821990827068176541032744152377606007460695865230455445490316090376844822501259106343706524194509410859747044301510282354678419831232665073515931614133865254324502750265996406483174791757276522461194898225654233114447953162193
h = 2116009228641574188029563238988754314114810088905380650788213482300513708694199075187203381676605068292187173539467885447061231622295867582666482214703260097506783790268190834638040582281613892929433273567874863354164328733477933865295220796973440457829691340185850634254836394529210411687785425194854790919451644450150262782885556693980725855574463590558188227365115377564767308192896153000524264489227968334038322920900226265971146564689699854863767404695165914924865933228537449955231734113032546481992453187988144741216240595756614621211870621559491396668569557442509308772459599704840575445577974462021437438528
c = 50609945708848823221808804877630237645587351810959339905773651051680570682896518230348173309526813601333731054682678018462412801934056050505173324754946000933742765626167885199640585623420470828969511673056056011846681065748145129805078161435256544226137963588018603162731644544670134305349338886118521580925
e = 65537
m = n ** 2 + 69420
a = pow(3, 1011, m)
b = pow(5, 1011, m)

B = matrix(ZZ, [[m, 0, 0], [a ^ 2, 1, 0], [b ^ 2, 0, 1]])

load("solver.sage")  # https://github.com/rkm0959/Inequality_Solving_with_CVP
lb = [h, 0, 0]
ub = [h, 2 ^ 1024, 2 ^ 1024]
result, applied_weights, fin = solve(B, lb, ub)  # PS: B will be modified inplace
v = vector(
    [x // y for x, y in zip(result, applied_weights)]
)  # closest vector to (lb+ub)/2
print(v)
if not v[1].is_square():
    R = B.LLL()
    l0 = vector([x // y for x, y in zip(R[0], applied_weights)])
    l1 = vector([x // y for x, y in zip(R[1], applied_weights)])
    # enumerate nearby vectors
    for i in range(-10, 10):
        for j in range(-10, 10):
            vv = v + l0 * i + l1 * j
            if vv[1].is_square():
                print("found", i, j)
                p = vv[1].sqrt()
                q = vv[2].sqrt()
                assert p * q == n
                d = inverse_mod(e, (p - 1) * (q - 1))
                m = power_mod(c, d, n)
                print(long_to_bytes(m))
# FLAG{7hI5_i5_4_C0MPL373_r4nD0M_fL49_8LinK}

easyRSA#

from Crypto.Util.number import *
import os

from flag import flag

blen = 256

def rsa(p: int, q: int, message: bytes):
	n = p * q
	e = 65537
	
	pad_length = n.bit_length() // 8 - len(message) - 2 # I padded too much
	message += os.urandom(pad_length)
	m = bytes_to_long(message)
	return (n, pow(m, e, n))

def level1(message1: bytes, message2: bytes):
	while True:
		p1 = getPrime(blen) # 512-bit number
		p2 = (p1 - 1) // 2
		if isPrime(p2):
			break

	q1 = getPrime(blen)
	q2 = getPrime(blen)

	return rsa(p1, q1, message1), rsa(p2, q2, message2)

def level2(message1: bytes, message2: bytes):
	while True:
		p1 = getPrime(blen) # 512-bit number
		p2 = (p1 + 1) // 2
		if isPrime(p2):
			break

	q1 = getPrime(blen)
	q2 = getPrime(blen)

	return rsa(p1, q1, message1), rsa(p2, q2, message2)

assert len(flag) == 44
l = len(flag) // 4
m1, m2, m3, m4 = [flag[i * l: i * l + l] for i in range(4)]
c1, c2 = level1(m1, m2)
c3, c4 = level2(m3, m4)

print(f'{c1 = }')
print(f'{c2 = }')
print(f'{c3 = }')
print(f'{c4 = }')

In this challenge, the flag is divided into four parts, each encrypted with a different RSA modulus. The first two are level1, and the last two are level2.

level1#

The solution starts with Fermat's Little Theorem $a^{p-1} \equiv 1 \pmod{p}$.

Even after raising to the $k$-th power, it holds $a^{k(p-1)} \equiv 1 \pmod{p}$.

Since $2n_2=2p_2q_2=(p_1-1)q_2$ is a multiple of $p_1-1$, $a^{2n_2} \equiv 1 \pmod{p_1}$, so $p_1 = \gcd(a^{2n_2}-1,n_1)$ holds for most $a$.

However, $n_2$ is a large number, making it impossible to raise any integer to the $2n_2$-th power without $\bmod{n_1}$. So, $p_1=\gcd((a^{2n_2}\bmod{n_1})-1,n_1)$.

This works because $p_1|n_1$. If it doesn't divide, this method won't work due to the following property:

This concept is similar to Pollard's p-1 method. When $p-1$ is smooth enough, multiplying by many small primes gives $R$. If $(p-1)|R$, raising to the $R$-th power allows factoring. This challenge uses $2n_2$ to provide a multiple of $p-1$ for easy factoring.

level2#

The only difference is that $p_1-1$ becomes $p_1+1$. Seeing $p_1+1$ reminds us of the Williams p+1 factorization method.

According to this article, for the following Lucas Sequence:

Let $D=A^2-4$. If $p \nmid D$, then $p \mid \gcd(V_m-2,n)$, where $m$ is a multiple of $p-\left(\dfrac{D}{p}\right)$, and $\left(\dfrac{D}{p}\right)$ is the Legendre symbol.

If $D$ is not a quadratic residue modulo $p$, then $\left(\dfrac{D}{p}\right)=-1$, so $m$ must be a multiple of $p+1$ to factor $p$. Since $2n_2=(p+1)q_2$ is a multiple of $p+1$.

$D=A^2-4$ can be guessed randomly, with about a $\frac{1}{2}$ chance of not being a quadratic residue. The remaining task is to calculate $V_{2n_2}$, which can be done modulo $n_1$ to avoid large numbers. Directly calculating $V_n$ using the recursive formula takes $\mathcal{O}(n)$, which is too slow for $2n_2$.

Noticing that $V_n$ is similar to the Fibonacci sequence, we can use matrix exponentiation to calculate the $n$-th term in $\mathcal{O}(\log{n})$, then use $\gcd$ to find $p_1$ and decrypt.

from Crypto.Util.number import *

c1 = (
    7125334583032019596749662689476624870348730617129072883601037230619055820557600004017951889099111409301501025414202687828034854486218006466402104817563977,
    4129148081603511890044110486860504513096451540806652331750117742737425842374298304266296558588397968442464774130566675039127757853450139411251072917969330,
)
c2 = (
    2306027148703673165701737115582071466907520373299852535893311105201050695517991356607853174423460976372892149320885781870159564414187611810749699797202279,
    600009760336975773114176145593092065538518609408417314532164466316030691084678880434158290740067228766533979856242387874408357893494155668477420708469922,
)
c3 = (
    9268888642513284390417550869139808492477151321047004950176038322397963262162109301251670712046586685343835018656773326672211744371702420113122754069185607,
    5895040809839234176362470150232751529235260997980339956561417006573937337637985480242398768934387532356482504870280678697915579761101171930654855674459361,
)
c4 = (
    6295574851418783753824035390649259706446806860002184598352000067359229880214075248062579224761621167589221171824503601152550433516077931630632199823153369,
    3120774808318285627147339586638439658076208483982368667695632517147182809570199446305967277379271126932480036132431236155965670234021632431278139355426418,
)
e = 65537


def solve_level1(n1, c1, n2, c2):
    p1 = gcd(power_mod(2, 2 * n2, n1) - 1, n1)
    p2 = (p1 - 1) // 2
    q1 = n1 // p1
    q2 = n2 // p2
    d1 = inverse_mod(e, (p1 - 1) * (q1 - 1))
    d2 = inverse_mod(e, (p2 - 1) * (q2 - 1))
    m1 = power_mod(c1, d1, n1)
    m2 = power_mod(c2, d2, n2)
    return long_to_bytes(m1), long_to_bytes(m2)


def lucas_v(a, n):
    # computes n-th lucas number for v_n=a*v_{n-1}-v_{n-2} with fast matrix power
    v0 = 2
    v1 = a
    R = a.base_ring()
    M = matrix(R, [[a, -1], [1, 0]])
    v = M ^ (n - 1) * vector(R, [v1, v0])
    return v[0]


def solve_level2(n1, c1, n2, c2):
    # based on Williams p+1: http://users.telenet.be/janneli/jan/factorization/williams_p_plus_one.html
    for a in range(2, 10):
        p1 = ZZ(gcd(lucas_v(Mod(a, n1), 2 * n2) - 2, n1))
        if 1 < p1 < n1:
            break
    p2 = (p1 + 1) // 2
    q1 = n1 // p1
    q2 = n2 // p2
    d1 = inverse_mod(e, (p1 - 1) * (q1 - 1))
    d2 = inverse_mod(e, (p2 - 1) * (q2 - 1))
    m1 = power_mod(c1, d1, n1)
    m2 = power_mod(c2, d2, n2)
    return long_to_bytes(m1), long_to_bytes(m2)


m1, m2 = solve_level1(*c1, *c2)
m3, m4 = solve_level2(*c3, *c4)

flag = b"".join([x[:11] for x in [m1, m2, m3, m4]])
print(flag)

# flag{S0rry_1_f0r9ot_T0_cH4nGe_7h3_t35t_fl46}

Extended Explanation#

The principle of Williams p+1 is to transfer operations to $\mathbb{Z}_n[i]/(i^2-T)$. This is similar to extending $\mathbb{R}$ to $\mathbb{C}$ with an $i$ satisfying $i^2+1=0$. If $\left(\dfrac{T}{p}\right)=-1$, then $i^2-T$ is irreducible, reducing to the field $\mathbb{F}_{p^2}$.

Since the multiplicative order of $\mathbb{F}_{p^2}$ is $(p^2-1)=(p+1)(p-1)$, there are different subgroups. Deriving, we find:

When raising to the $p+1$-th power, the imaginary part disappears, indicating it's a multiple of $p$, allowing factoring with gcd.

If $\left(\dfrac{T}{p}\right)=1$, then $i^p=i$, so:

The imaginary part still disappears, allowing factoring with gcd. This means Williams p+1 can also handle the p-1 case. However, Pollard p-1 uses the known real part $1$ for gcd.

Using sage for a simple verification:

p = random_prime(2 ^ 512)
q = random_prime(2 ^ 512)
n = p * q
P.<x> = Zmod(n)[]


def test(T):
    print("QR", kronecker(T, p))
    R.<i> = P.quotient(x^2 - T)
    z = 1 + i
    print("p-1", gcd((z ^ (p - 1))[1], n))
    print("p+1", gcd((z ^ (p + 1))[1], n))


T = next(x for x in range(2, 100) if kronecker(x, p) == 1)
test(T)
T = next(x for x in range(2, 100) if kronecker(x, p) == -1)
test(T)

The original Williams p+1 uses the Lucas sequence to achieve the same goal, calculating high powers in $\mathbb{Z}_n[i]/(i^2-T)$.

For the characteristic polynomial $x^2-Ax+1$ of this sequence, we find two roots and use the initial terms to solve for constants $c_1=c_2=1$, giving the general term formula:

Considering $\bmod{p}$, we find $D=A^2-4$ is the $T$, determining whether it's $p+1$ or $p-1$. For $\left(\dfrac{T}{p}\right)=-1$, we derive:

Multiplying by a multiple of $p+1$ gives the same result, so $\gcd(V_{c(p+1)}-2,n)$ yields $p$.

This article provides a more advanced mathematical explanation, but I couldn't fully understand the latter part...

notPRNG#

from secret import flag
import sys

def genModular(x):
    if x <= 2 * 210:
        return random_prime(2^x, False, 2^(x - 1))
    return random_prime(2^210, False, 2^209) * genModular(x - 210)

N, L = 100, 200
M = genModular(int(N * N * 0.07 + N * log(N, 2)))

# generate a random vector in Z_M
a = vector(ZZ, [ZZ.random_element(M) for _ in range(N)])

# generate a random 0/1 matrix
while True:
    X = Matrix(ZZ, L, N)
    for i in range(L):
        for j in range(N):
            X[i, j] = ZZ.random_element(2)
    if X.rank() == N:
        break

# let's see what will this be
b = X * a
for i in range(L):
    b[i] = mod(b[i], M)

print('N =', N)
print('L =', L)
print('M =', M)
print('b =', b)

x = vector(ZZ, int(N))
for j in range(N):
    for i in range(L):
        x[j] = x[j] * 2 + X[i, j]



def bad():
    print("They're not my values!!!")
    sys.exit(0)

def calc(va, vx):
    ret = [0] * L
    for i, vai in enumerate(va):
        for j in range(L):
            bij = (vx[i] >> (L - 1 - j)) & 1
            ret[j] = (ret[j] + vai * bij) % M
    return ret


if __name__ == '__main__':
    print('What are my original values?')
    print('a?')
    aa = list(map(int, input().split()))
    print('x?')
    xx = list(map(int, input().split()))

    if len(aa) != len(a):
        bad()
    if len(xx) != len(x):
        bad()
    if calc(a, x) != calc(aa, xx):
        bad()

    print(flag)

The code is complex, but simply put, it gives a vector $b$ and a large integer $M$, and asks for a matrix $X$ and a vector $a$ such that $Xa \equiv b \pmod{M}$. Each element of $X$ can only be $0,1$, and $\operatorname{rank}(X)=N$.

The following part of the source code compresses the $0,1$ matrix $X$:

x = vector(ZZ, int(N))
for j in range(N):
    for i in range(L):
        x[j] = x[j] * 2 + X[i, j]

The calc function uses the compressed matrix vx and vector va to compute $Xa \pmod{M}$.

This problem's $X$ is an $L \times N$ matrix, $a$ is an $N \times 1$ vector, and $b$ is an $L \times 1$ vector, with $L=200,N=100$. If $N=L=200$, a trivial solution is $X$ as the identity matrix $I_n$ and $a=b$. However, the challenge is that $N<L$.

This problem asks how to decompose an $L$-dimensional $b$ vector into $N$ basis vectors composed of $0,1$. Initially, I couldn't think of a solution. However, if $a$ is known, the problem becomes solving $L$ subset sum problems. Although this problem is NP-Complete in general, it can be solved in polynomial time using algorithms like LLL in low-density cases. (Solving Low-Density Subset Sum Problems)

Given the generation method of $M$, the density is:

For subset sum problems with density less than $0.9408$, LLL can handle them (source), so this problem is related to LLL.

There are two approaches: finding $X$ first or $a$ first. I don't know how to find $a$ first, but fixing $a$ doesn't guarantee a subset sum solution. Even if a solution exists, solving $L$ subset sums takes about 20 seconds each on my computer, totaling $20 \times 200$ seconds, which would timeout, so this approach is infeasible.

The other approach is finding $X$ first, then solving for $a$. However, not all $0,1$ matrices have solutions. The goal is to find a method to obtain $X$, even if $X'$ differs from the original $X$, as long as it can solve for $a'$ such that $X'a' \equiv b \pmod{M}$.

First, reduce the following Lattice:

where the blank parts are $0$, and $T$ is a large constant to keep the first dimension of the reduced basis small. The reduced basis will have multiple short vectors $v=(0,k_0,k_1,...,k_{L-